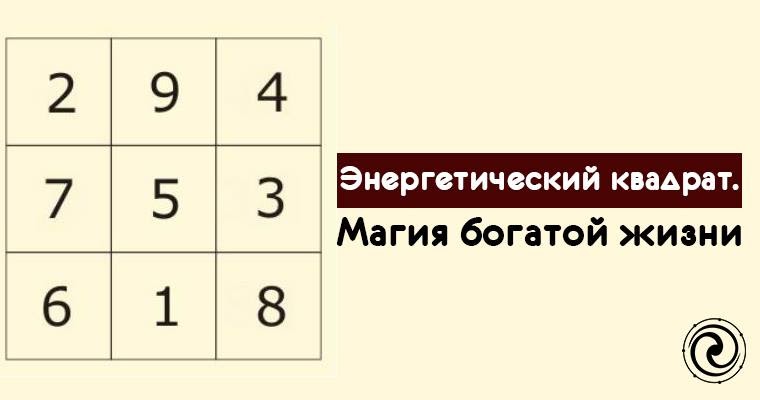
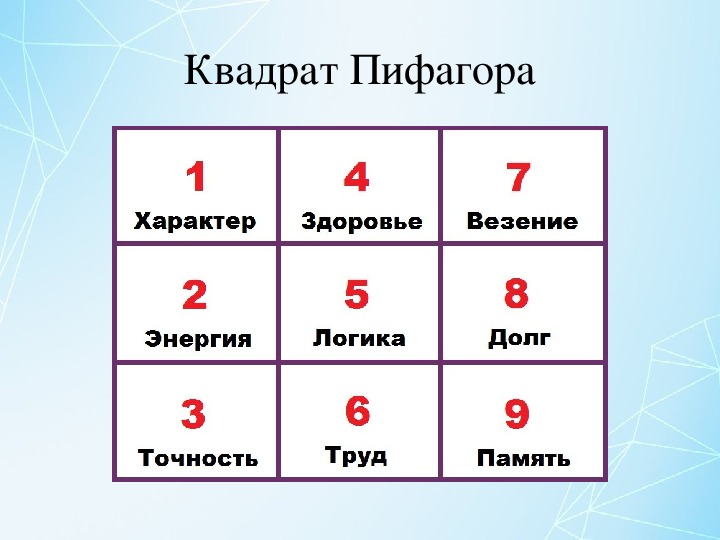
Как сделать личный денежный талисман «Магический квадрат Пифагора»?
Однажды Пифагор составил магический квадрат, который способен «притягивать» энергию денег, богатства. «Магнит» для здоровья, богатства и благополучия… И между прочим, квадратом Пифагора пользовался сам великий Генри Форд. Он начертил его на долларовой купюре и всегда носил в потайном отделении бумажника как талисман. Его даже называют Квадрат Форда. А на бедность, как известно, Форд не жаловался. В возрасте 83 лет Генри передал бразды правления огромной корпорацией и своё немалое состояние в размере 1 млрд. долларов (а с учётом инфляции — более 36 млрд по нынешним ценам) своим внукам.
Цифры, особым образом вписанные в квадрат, способны не только притянуть богатство. Например, великий врач Парацельс составил свой квадрат — «талисман здоровья». В общем, если грамотно построить магический квадрат, можно впустить в жизнь те энергетические потоки, которые вам необходимы.
Как сделать личный талисман магический квадрат Пифагора? Надеюсь, вы умеете писать цифры и считать до десяти? Тогда вперед. Чертим энергетический квадрат, который может стать вашим личным талисманом.
Чертим энергетический квадрат, который может стать вашим личным талисманом.
В нем три колонки и три ряда. Всего девять цифр, которые составляют ваш индивидуальный нумерологический код.
Как вычислить этот код?
Как вычислить этот код?
В первый ряд поставим три цифры:
цифру вашего дня рождения,
месяца рождения
года рождения.
Например, вы появились на свет 25 мая 1971 года. Тогда ваше первое число — число дня: 25. Это сложное число, по законам нумерологии, его надо сократить до простого, сложив цифры 2 и 5. Получается — 7: вот семерку мы и поставим в первую клеточку квадрата.
Второе — число месяца: 5, ведь май — пятый месяц. Обратите внимание: если человек родился в декабре, то есть в месяце под номером 12, нам бы пришлось сокращать число до простого: 1+2 = 3.
Третье — число года. Тут уж сокращать до простого придется всем. Итак: 1971 (год рождения) раскладываем на составные цифры и считаем их сумму. 1+9+7+1 = 18, 1+8 =9.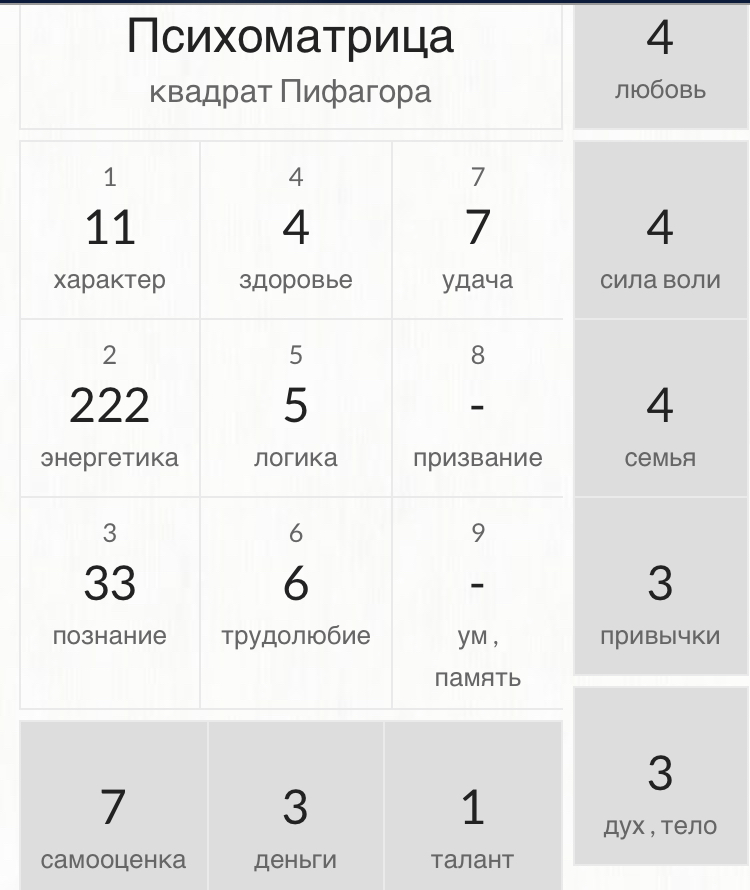
Вписываем в первый ряд цифры: 7, 5, 9.
Во второй ряд поставим цифры:
четвертая — вашего имени,
пятая — отчества,
шестая — фамилии.
Их определяем по таблице буквенно-цифровых соответствий.
Руководствуясь ею, вы складываете цифровые значения каждой буквы своего имени, при необходимости приводите сумму к простому числу.
Точно также действуем с отчеством и фамилией.
Например, Кротов= 3+9+7+2+7+3=31=3+1=4
Теперь у нас имеется три цифры для второй строки энергетического квадрата
Третий ряд
Чтобы заполнить третий ряд, найти седьмую, восьмую и девятую цифры, придется обратиться к астрологии.
Седьмая цифра — номер вашего знака Зодиака.
Тут все просто. Овен — первый знак, ему соответствует цифра 1. Рыбы — двенадцатый знак, им соответствует цифра 12.
Внимание: в данном случае сокращать двузначные цифры до простых не следует, числа 10, 11 и 12 имеют собственное значение!
Восьмая цифра — номер вашего знака по Восточному календарю. Найти его несложно по таблице ниже:
Найти его несложно по таблице ниже:
То есть, если вы родились в 1974 году, номер вашего знака — 3 (Тигр), а если в 1982 году — 11 (Собака).
Девятая цифра — нумерологический код вашего желания.
Например, вы набираете энергию ради здоровья. Значит, ключевое слово — «здоровье». Складываем буквы снова по первой таблице:
З — 9, Д — 5, О — 7, Р — 9, О — 7, В — 3, Ь — 3, Е — 6 = 49, то есть 4+9=13. Поскольку у нас снова получилось сложное число, продолжаем сокращать: 1+3=4
Имейте в виду: если у вас получились числа 10, 11 и 12, то и в этом случае их сокращать не следует.
Ну а если вам не хватает денег, то вы можете высчитать значение слов «богатство», «деньги» или конкретно «доллар», «евро».
Итак, последней девятой цифрой в вашем магическом квадрате будет число — нумерологическое значение вашего ключевого слова или другими словами код желания.
Спойте свою денежную «квадратную» медитацию
А теперь расположим девять цифр в три ряда по три цифры в нашем магическом квадрате.
Нарисованный квадрат можно вставить в рамку и повесить дома или в офисе. Можно положить в кошелёк. А можно спрятать в папочку, убрать подальше от посторонних глаз. Прислушайтесь к своему внутреннему голосу, он подсказывает, что подходит именно вам.
Но и это еще не все. Выучите цифры своего личного нумерологического кода в той последовательности, как они стоят в клеточках. Зачем? Это ваша личная мантра, ваша прямой провод с Богом, если хотите. Она настраивает вас на нужный поток из огромного множества сил во Вселенной, а с другой стороны — вас слышат и отвечают на ваши вибрации.
Поэтому свою мантру надо выучить наизусть. И — медитировать. Повторяя мысленно свой нумерологический код, сядьте в удобное кресло или прилягте на диван. Расслабьтесь. Руки держите ладонями вверх, как бы принимая энергию. Через некоторое время вы ощутите покалывание в пальцах, вибрацию, может быть — тепло или, напротив, холодок в ладонях.
Отлично: энергия пошла! Медитация длится до тех пор, пока вам не захочется ее прекратить.
Я покажу свой вариант квадрата Пифагора, но вы, конечно, должны сделать свой. Для этого есть автоматизированный сервис, чтобы облегчить вам задачу.
А все мои деньги я успешно считаю здесь уже с 2008 года
Денежный талисман «Магический Квадрат Пифагора»
Магический денежный талисман «Квадрат Пифагора» работает с мощной энергией – это сильный магнит для привлечения богатства и финансового благополучия. Великий математик Пифагор всю свою жизнь посвятил изучению науки нумерологии. Одним из его потрясающих достижений стало изобретение магического квадрата.
Уникальная фигура сможет поменять всю вашу жизнь. Она подарит вам желаемое – кому здоровье, кому удачу, а кому безмерное богатство.
Уникальность и магическая сила квадрата Пифагора в том, что сумма чисел во всех столбцах, рядах и диагоналях, приведенная к однозначному, равна 6.
Например: средний столбец (9+5+1=15=1+5=6)
Средняя линия (3+5+7=15=1+5=6)
Диагональ слева низ: (8+5+2=15=1+5=6)
Уже не одно столетие магические квадраты для привлечения денег активно работают на благо человечества. И у вас есть уникальная возможность на себе ощутить их положительный эффект.
И у вас есть уникальная возможность на себе ощутить их положительный эффект.
Содержание
- Как работает
- Как сделать для привлечения денег
- Магический квадрат исполнения желаний
- Денежные талисманы миллионеров
Как работает
Большое значение имеет отношение носителя к своему счастливому предмету. Если вы не намерены полностью ему доверять, то не рассчитывайте на дополнительную помощь – магия не будет работать.
Как же действует магический квадрат желаний, разработанный Пифагором? Попробуем разобраться.
Благодаря собственному магнетизму он притягивает финансовую энергию и удерживает ее около себя. Причиной многих денежных неудач является дефицит звеньев в персональной денежной цепочке. Талисман постепенно восстанавливает баланс и ремонтирует энергетические расколы.
Обладатель магического символа полностью открыт для новых денежных потоков – его положение улучшается, а проблемы рассыпаются одна за другой. И секрет успешности кроется в небольшом личном амулете.
И секрет успешности кроется в небольшом личном амулете.
Когда вы начнете использовать силу денежного талисмана, вы добьетесь следующих результатов:
- укрепите свое состояние и никогда не будете ощущать нехватки денег;
- в вашем доме появится много новых дорогих вещей;
- работа начнет радовать и приносить хорошие доходы;
- каждое новое дело будет успешным;
- вы защитите себя от нечестных обманщиков и мошенников;
- также вам будут нестрашны ни сглазы, ни проклятия.
Как сделать для привлечения денег
Вы можете самостоятельно создать магический квадрат на деньги – это совсем несложно.
Возьмите чистый лист бумаги и нарисуйте на нем квадрат – это и есть энергетическая основа вашего оберега. Разделите его на девять равных квадратиков – в каждом будет написана особенная цифра.
Теперь вам необходимо вычислить персональные девять чисел (сверху вниз начиная с левого столбика).
- Первое: ваша дата рождения. Если это двузначное число – сведите его к простому путем суммирования (например: 25=2+5=7).
- Второе: месяц рождения. Если вы родились в октябре, ноябре или декабре, то приведите число месяца рождения к однозначному.
- Третье: год рождения. Также разложите число года на простые и сложите.
- Четвертое: имя. При помощи специальной таблицы переведите буквы своего имени в цифры – и также сведите к простому.
- Пятое: отчество. Повторяем ту же процедуру, что и в предыдущем пункте.
- Шестое: фамилия. И снова – повторите все действия.
- Седьмое: знак Зодиака. В этом случае не стоит упрощать число до однозначного – это важный момент!
- Восьмое: число вашего года рождения по Восточному календарю. Выберите его из специальной таблицы ниже:
- Девятое: номер вашего желания.
 Здесь понадобится табличка соответствия цифр и букв. Если ваше желание «Деньги» – переведите все буквы слова в числа, сложите и приведите к однозначному.
Здесь понадобится табличка соответствия цифр и букв. Если ваше желание «Деньги» – переведите все буквы слова в числа, сложите и приведите к однозначному.
Теперь ваш денежный талисман полностью готов. Теперь поступите так, как подскажет вам сердце. Некоторые вешают магический квадрат Пифагора у всех на виду, а некоторые – прячут от чужих глаз.
Магический квадрат исполнения желаний
Каждый персональный амулет – это необычный предмет. Он обладает особенными свойствами и привлекает к своему обладателю счастье и удачу.
В первую очередь талисман работает с энергетическими волнами. Когда человек активирует его биополе, он получает огромную поддержку Вселенной. Это помогает раскрыть в себе новые таланты и способности.
Самые заветные мечты могут сбыться, если правильно пользоваться магическим квадратом Пифагора.
Его особенностью является то, что расчеты основаны на дате рождения человека. Это усиливает энергетику предмета в несколько раз. Он соединяется с биополем своего обладателя и помогает стать успешнее во всех делах.
Он соединяется с биополем своего обладателя и помогает стать успешнее во всех делах.
И речь идет не только о деньгах – мистические числа подарят вам то, что вы пожелаете: здоровье, благополучие, хорошую работу. Вы обретете счастье – стоит лишь попросить об этом Вселенную.
Денежные талисманы миллионеров
Многим успешным людям личные денежные талисманы помогли добиться поставленных целей.
Изучая биографии самых известных миллионеров, можно встретить очень интересный факт – практически каждый имел свой личный оберег. На протяжении всей жизни они обращались к помощи энергетического символа.
Вот несколько примеров.
- Джон Рокфеллер доверял волшебству неразменной купюры, которую бережно хранил в специальной коробочке.
- Генри Форд пользовался квадратом Пифагора – свидетели утверждают, что он чертил его на долларовых банкнотах.
- Сэнди Слоу никогда не расставался с пентаклем Соломона – древнейшим символом власти и богатства.
 Эта пентаграмма особенная, так как соединяет в себе силы всех пяти жизненных стихий.
Эта пентаграмма особенная, так как соединяет в себе силы всех пяти жизненных стихий.
Алена Головина — белая ведунья, магистр Космоэнергетики, автор сайта «МАГиЯ»
Интересное по теме:
- Магические предметы и артефакты
- Талисман Венеры — символ любви
- Японские талисманы, обереги и амулеты
Понравилась статья?
Теорема Пифагора | Определение и история
Теорема Пифагора
Смотреть все СМИ
- Ключевые люди:
- Евклид
- Похожие темы:
- Евклидова геометрия
Пифагорейская тройка
число Пифагора
Ветряная мельница Евклида
Просмотреть весь соответствующий контент →
Резюме
Прочтите краткий обзор этой темы
Теорема Пифагора , известная геометрическая теорема о том, что сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы (стороне, противоположной прямому углу) — или, в привычной алгебраической записи, а 2 + б 2 = в 2 . Хотя эта теорема долгое время ассоциировалась с именем греческого математика и философа Пифагора (ок. 570–500/490 до н. э.), на самом деле она намного старше. Четыре вавилонские таблички ок. 19 г.00–1600 г. до н.э. указывают на некоторое знание теоремы с очень точным вычислением квадратного корня из 2 (длина гипотенузы прямоугольного треугольника с длиной обоих катетов, равной 1) и списками специальных целых чисел, известных как пифагорейские. тройки, удовлетворяющие ему (например, 3, 4 и 5; 3 2 + 4 2 = 5 2 , 9 + 16 = 25). Теорема упоминается в индийской Баудхаяне Сульба-сутре , написанной между 800 и 400 г. до н.э. Тем не менее, теорема стала приписываться Пифагору. Это также предложение номер 47 из Книги I Евклида 9.0027 Элементы .
Хотя эта теорема долгое время ассоциировалась с именем греческого математика и философа Пифагора (ок. 570–500/490 до н. э.), на самом деле она намного старше. Четыре вавилонские таблички ок. 19 г.00–1600 г. до н.э. указывают на некоторое знание теоремы с очень точным вычислением квадратного корня из 2 (длина гипотенузы прямоугольного треугольника с длиной обоих катетов, равной 1) и списками специальных целых чисел, известных как пифагорейские. тройки, удовлетворяющие ему (например, 3, 4 и 5; 3 2 + 4 2 = 5 2 , 9 + 16 = 25). Теорема упоминается в индийской Баудхаяне Сульба-сутре , написанной между 800 и 400 г. до н.э. Тем не менее, теорема стала приписываться Пифагору. Это также предложение номер 47 из Книги I Евклида 9.0027 Элементы .
Согласно сирийскому историку Ямвлиху (ок. 250–330 гг. н. э.), Пифагора познакомили с математикой Фалес Милетский и его ученик Анаксимандр. В любом случае известно, что Пифагор отправился в Египет около 535 г. до н. э. для продолжения своих исследований, был захвачен во время вторжения Камбиса II из Персии в 525 г. до н. э. и доставлен в Вавилон, и, возможно, посетил Индию, прежде чем вернуться в Средиземное море. Пифагор вскоре поселился в Кротоне (ныне Кротоне, Италия) и основал школу, или, говоря современным языком, монастырь (9).0027 см. Пифагорейство), где все члены дали строгий обет секретности, а все новые математические результаты на протяжении нескольких столетий приписывались его имени. Таким образом, не только неизвестно первое доказательство теоремы, но и есть некоторые сомнения в том, что сам Пифагор действительно доказал теорему, носящую его имя. Некоторые ученые предполагают, что первым доказательством было то, что показано на рисунке. Вероятно, он был независимо обнаружен в нескольких разных культурах.
до н. э. для продолжения своих исследований, был захвачен во время вторжения Камбиса II из Персии в 525 г. до н. э. и доставлен в Вавилон, и, возможно, посетил Индию, прежде чем вернуться в Средиземное море. Пифагор вскоре поселился в Кротоне (ныне Кротоне, Италия) и основал школу, или, говоря современным языком, монастырь (9).0027 см. Пифагорейство), где все члены дали строгий обет секретности, а все новые математические результаты на протяжении нескольких столетий приписывались его имени. Таким образом, не только неизвестно первое доказательство теоремы, но и есть некоторые сомнения в том, что сам Пифагор действительно доказал теорему, носящую его имя. Некоторые ученые предполагают, что первым доказательством было то, что показано на рисунке. Вероятно, он был независимо обнаружен в нескольких разных культурах.
Британская викторина
Тест «Все о математике»
Ваш учитель алгебры был прав. Вы будете использовать математику после выпуска — для этой викторины! Посмотрите, что вы помните из школы, и, возможно, узнаете несколько новых фактов в процессе.
Книга I из Элементов заканчивается знаменитым «ветряным» доказательством теоремы Пифагора Евклида. ( См. Врезка: Ветряная мельница Евклида.) Позже, в Книге VI Элементов , Евклид предлагает еще более простую демонстрацию, используя предположение, что площади подобных треугольников пропорциональны квадратам их соответствующих сторон. По-видимому, Евклид изобрел доказательство ветряной мельницы, чтобы поместить теорему Пифагора в качестве краеугольного камня Книги I. Он еще не продемонстрировал (как он сделал бы в Книге V), что длинами линий можно управлять в пропорциях, как если бы они были соизмеримыми числами ( целые числа или отношения целых чисел). Проблема, с которой он столкнулся, объясняется во врезке: Несоизмеримые.
Придумано великое множество различных доказательств и расширений теоремы Пифагора. Взяв сначала расширения, сам Евклид показал в прославленной в древности теореме, что любые симметричные правильные фигуры, нарисованные на сторонах прямоугольного треугольника, удовлетворяют пифагорову соотношению: фигура, нарисованная на гипотенузе, имеет площадь, равную сумме площадей фигур.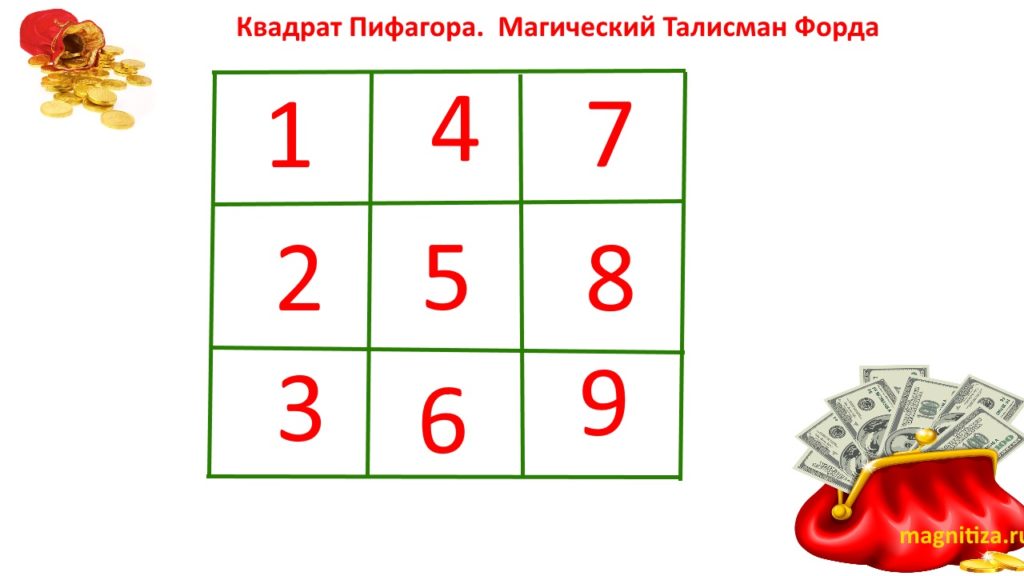 рисуется на ногах. Полукруги, которые определяют гиппократовские луны Хиоса, являются примерами такого расширения. ( См. Врезка: Квадратура луны.)
рисуется на ногах. Полукруги, которые определяют гиппократовские луны Хиоса, являются примерами такого расширения. ( См. Врезка: Квадратура луны.)
В Девяти главах по математическим процедурам (или Девять глав ), составленных в 1 веке н.э. в Китае, дано несколько задач вместе с их решениями, которые включают в себя нахождение длины одной из сторон прямоугольного треугольника по двум другим сторонам. В Комментарии Лю Хуэя , относящемся к 3 веку, Лю Хуэй предложил доказательство теоремы Пифагора, которая призывала разрезать квадраты на катетах прямоугольного треугольника и переставлять их («стиль танграма»), чтобы они соответствовали квадрат на гипотенузе. Хотя его оригинальный рисунок не сохранился, на следующем рисунке показана возможная реконструкция.
Теорема Пифагора очаровывала людей почти 4000 лет; сейчас существует более 300 различных доказательств, в том числе греческого математика Паппа Александрийского (расцвет творчества ок. 320 г. н. э.), арабского математика-физика Табита ибн Курраха (ок. 836–901 гг.), итальянского художника-изобретателя Леонардо да Винчи. (1452–1519) и даже президент США. Джеймс Гарфилд (1831–1881).
320 г. н. э.), арабского математика-физика Табита ибн Курраха (ок. 836–901 гг.), итальянского художника-изобретателя Леонардо да Винчи. (1452–1519) и даже президент США. Джеймс Гарфилд (1831–1881).
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена Эриком Грегерсеном.
Ветряная мельница Евклида | Britannica
Теорема Пифагора утверждает, что сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы (стороне, противоположной прямому углу) — в привычных алгебраических обозначениях a 2 + б 2 = в 2 . Вавилоняне и египтяне нашли несколько целочисленных троек ( a , b , c ), удовлетворяющих соотношению. Пифагор (ок. 580–ок. 500 до н. э.) или один из его последователей, возможно, был первым, кто доказал теорему, носящую его имя. Евклид (ок. 300 г. до н. э.) предложил искусную демонстрацию теоремы Пифагора в своем труде 9.0027 Элементы , известные как доказательство ветряной мельницы из-за формы фигуры.
Евклид (ок. 300 г. до н. э.) предложил искусную демонстрацию теоремы Пифагора в своем труде 9.0027 Элементы , известные как доказательство ветряной мельницы из-за формы фигуры.
Нарисуйте квадраты по бокам справа Δ A B C .
B C H и A C K — прямые линии, потому что ♂ A C B = C B = .
∠ E A B = ∠ C A I = 90°, по построению.
секрет B A I = ▲ B A C +R C A I = C A I = C A I = C A I = C A I . E A B = ∠ E A C , by 3.

A C = A I and A B = A E , по конструкции.
Следовательно, Δ B A I ≅ Δ E A C , как выделено в части теоремы о боковом углу: боковой мост (см. (а) рисунка.
Начертить C F параллельно B D .
Прямоугольник A G F E = 2Δ A С Е . Этот замечательный результат вытекает из двух предварительных теорем: (а) площади всех треугольников с одним и тем же основанием, третья вершина которых лежит в любом месте на бесконечно продолженной прямой, параллельной основанию, равны; и (b) площадь треугольника составляет половину площади любого параллелограмма (включая любой прямоугольник) с тем же основанием и высотой.
Квадрат A I H C = 2Δ B A I , по той же теореме параллелограммы, что и на шаге 8.

Следовательно, прямоугольник A G F E = Square A I H A I H A I H C I H C , H C , H C , H C . 8, and 9.
∠ D B C = ∠ A B J , as in steps 3 and 4.
B C = B J и B D = A B , by construction as in step 5.
Δ C B D ≅ Δ J B A , as in step 6 and выделены в части (b) рисунка.
Прямоугольник B D F G = 2Δ C B D , как на шаге 8.

- 19 D , как на этапе 8.
- 11128 7 C C C C C C C 7 C 7 C 7 C 7 C C C .0028 B = 2Δ J B A , as in step 9.
Therefore, rectangle B D F G = square C K J B , as in step 10.
Square A B D E = rectangle A G F E + rectangle B D Ф G , по конструкции.
Следовательно, квадрат A B D E = Square A I H C +Square C . 10 и 16.
Первая книга Евклида Элементы начинается с определения точки и заканчивается теоремой Пифагора и ее обращением (если сумма квадратов на двух сторонах треугольника равна квадрату на третья сторона, это должен быть прямоугольный треугольник).
 Здесь понадобится табличка соответствия цифр и букв. Если ваше желание «Деньги» – переведите все буквы слова в числа, сложите и приведите к однозначному.
Здесь понадобится табличка соответствия цифр и букв. Если ваше желание «Деньги» – переведите все буквы слова в числа, сложите и приведите к однозначному.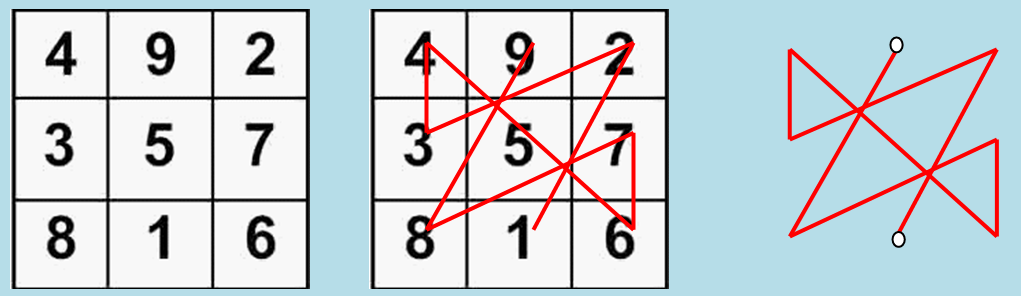 Эта пентаграмма особенная, так как соединяет в себе силы всех пяти жизненных стихий.
Эта пентаграмма особенная, так как соединяет в себе силы всех пяти жизненных стихий.