Как понять пойдет ли каре: Beauty-тест: Как понять, что вам пойдет короткая стрижка?

Содержание

Как определить пойдет ли вам 🚩 короткая стрижка

✅ То ли жизнь изменить, то ли стрижку… Примерно так начинается каждая новая страница в жизни типичной женщины.

❎ Не буду отрицать, прическа играет для нас огромную роль и обладает почти магической силой менять настроение, внутреннее состояние и даже обстоятельства.

Ну, и по старой женской традиции, прическу мы меняем примерно по схеме: “длинные волосы – подстричь, короткие – нарастить, прямые – завить, а кудрявые – выпрямить”.

Ничего не поделаешь – натура такая. Но, если вы решаетесь сесть в кресло парикмахера, будучи Рапунцель, а встать оттуда с каре или бобом, то должны понимать, сколь велик риск остаться недовольной.

К счастью, есть способ…

О котором знают немногие. Его автор – Джон Фрида – известный британский стилист-парикмахер, работавший в свое время с такими звездами как Жаклин Кеннеди и Дайана Росс, Полл МакКартни и принцесса Диана. В общем доверять таком мэтру можно.

Суть метода в том, чтобы определить пропорции лица, в частности – высоту челюстной кости. Для этого измерьте расстояние между мочкой уха и кончиком подбородка. Возьмите карандаш и линейку. Приложите их друг к другу так, как показано на рисунке, т.е. под прямым углом.

Если расстояние меньше 5,7 см, вам пойдут короткие стрижки, смело идите в салон. Если больше – то ваше лицо будет смотреться выгоднее и красивее всего в обрамлении длинных волос.

И еще несколько советов:

Совет #1: Учитывайте форму вашего лица

Короткие стрижки могут подойти любой форме лица, за исключением круглой. Женщинам с круглым лицом больше подходят стрижки ниже уровня плеч. Боб на круглой форме лица смотрится, как каска. В таком случае необходимо зрительно удлинять лицо, и поэтому оставлять длину волос.

Совет #2: У вас красивые плечи, подбородок и шея?

Короткие волосы непременно подчеркнут их. Если у вас короткая шея, двойной подбородок или широкие плечи, подстригать волосы выше ключицы не стоит.

Совет #3: У вас вьющиеся волосы? Подумайте дважды

Вьющиеся волосы имеют тенденцию пушиться, если имеют короткую длину. Некоторые стилисты утверждают, что вьющиеся волосы должны быть подстрижены не короче, чем на пять сантиметров ниже подбородка, но я встречала роскошные варианты коротких стрижек на кудрявых волосах.

Секрет в многослойности. Подстригать вьющиеся волосы – это искусство, поэтому тщательно выбирайте стилиста, чтобы после посещения салона не быть похожей на пуделя.

Совет #4: Тонкие волосы смотрятся лучше в коротких стрижках

Очень тонкие волосы выглядят плоскими, если имеют большую длину. Если у вас тонкие или жидкие волосы, короткая стрижка добавит им объем, только будьте осторожны со слоями. Старайтесь сохранить все волосы одной длины, на сколько это возможно. Большое количество обрезанных волос может сказаться на объеме.

Совет #5: Уловка

Я нашла этот совет в «Признании редактора по красоте» журнала Allure, Динды Вэллс (Linda Wells). Возьмите свою фотографию, чтобы на заднем плане было светло или темно, в зависимости от цвета ваших волос (если вы блондинка, выбирайте темный задний план, если брюнетка – светлый).

Возьмите ножницы и подстригайте волосы на фотографии, чтобы увидеть, пойдет ли вам короткая стрижка или нет. Мы советуем начать с более длинных волос, чтобы не растрачивать фотографию.

Beauty-тест: Как понять, что вам пойдет короткая стрижка? : lazzo_fiaba — LiveJournal

Categories:

Здоровье
catIsShown({ humanName: ‘косметика’ })» data-human-name=»косметика»> Косметика
Cancel

Этот метод придумал известный парикмахер Джон Фрида, основавший собственную линию ухода за волосами. А я прочитала о нём на сайте журнала Elle.

Вам потребуется только линейка и карандаш. Встаньте к зеркалу в профиль, приложите карандаш к подбородку горизонтально и измерьте расстояние от карандаша до мочки уха.

Если расстояние 5,7 сантиметра (2,25 дюйма) и меньше, можете смело стричься, — короткие волосы вам точно пойдут. Если больше — эксперимент скорее всего не удастся.

Tags: волосы, дамские штучки

Макияж Эмилии Кларк: фэйлы и удачи
Потому что Эмилия Кларк ужасно красится (с) — написал на форуме Экслера, где я обсуждаю «Игру престолов» один товарищ. Прав ли он? Частично прав, но…
Проф! Маска для волос L’Oreal Professionnel Expert Intense Repair
Маска–уход Интенс Репер создана для ухода за сухими, безжизненными и ослабленными волосами. Входящие в состав маски керамиды способствуют…
Бюджетно! MAYBELLINE ПАЛЕТКА ТЕНЕЙ THE NUDES
Не все себе могут позволить легендарную палитру теней Urban Decay Naked, о которой я тоже когда-нибудь напишу, но, по счастью, масс-маркет…

Photo

Hint http://pics.livejournal.com/igrick/pic/000r1edq

15 comments

15 comments

Макияж Эмилии Кларк: фэйлы и удачи
Потому что Эмилия Кларк ужасно красится (с) — написал на форуме Экслера, где я обсуждаю «Игру престолов» один товарищ. Прав ли он? Частично прав, но…
Проф! Маска для волос L’Oreal Professionnel Expert Intense Repair
Маска–уход Интенс Репер создана для ухода за сухими, безжизненными и ослабленными волосами. Входящие в состав маски керамиды способствуют…
Бюджетно! MAYBELLINE ПАЛЕТКА ТЕНЕЙ THE NUDES
Не все себе могут позволить легендарную палитру теней Urban Decay Naked, о которой я тоже когда-нибудь напишу, но, по счастью, масс-маркет…

Платежные споры Процесс | Центр поддержки Square

Обновления системы

Подождите, пока банк разрешит дело

После того, как ваша документация будет отправлена в Square через панель управления спорами, мы проверим вашу документацию и перешлем вашу информацию в банк вашего клиента. На панели управления спорами или на мобильном устройстве вы также можете просмотреть статус спора, все загруженные вами документы и дальнейшие действия в процессе спора.

Примечание . В настоящее время отслеживание споров доступно только на устройствах iOS.

Примечание: После того, как банк примет решение, исход спора будет окончательным — Square больше не сможет оспаривать спор от вашего имени. Если вы хотите продолжить рассмотрение дела, вам необходимо решить его напрямую с вашим клиентом или обратиться в суд.

Отмена споров

Если вы и ваш клиент решаете спор напрямую до того, как банк примет решение, вы можете попросить клиента связаться с его банком, чтобы отменить спор. Отмену можно запросить в любое время в процессе спора, прежде чем он будет закрыт.

Передовой опыт

У вас больше шансов избежать споров, а когда они все же случаются, убедить банк вашего клиента в своей правоте, следуя нескольким рекомендациям.

Примечание: Square не имеет никакого влияния и не определяет разрешение процесса возврата платежа и может только поддержать продавца, помогая представить обоснованное дело для рассмотрения.

Узнайте больше о : Обработка платежей

Помогите нам улучшить наш Центр поддержки. Была ли эта статья полезной?

Как мы можем улучшить эту статью?

Этот отзыв используется только для улучшения этой статьи Центра поддержки и не отправляется в нашу службу поддержки. Вопросы, требующие ответа, можно отправить по ссылке вверху этой страницы.

Спасибо за положительный отзыв!

Спасибо, мы поработаем над улучшением этой статьи.
Есть вопрос? Свяжитесь с нами.

Не можете найти то, что вам нужно?

Спросите нашего помощника по поддержке

Репетиторство по математике для экспертов в Великобритании

Квадратный корень числа — это операция, обратная возведению числа в квадрат. Квадрат числа — это значение, которое получается, когда мы умножаем число само на себя, а квадратный корень из числа получается путем нахождения числа, которое при возведении в квадрат дает исходное число.

Если «а» — это квадратный корень из «b», это означает, что a × a = b. Квадрат любого числа всегда является положительным числом, поэтому каждое число имеет два квадратных корня, один из которых имеет положительное значение, а другой — отрицательное. Например, и 2, и -2 являются квадратными корнями из 4. Однако в большинстве случаев только положительное значение записывается как квадратный корень из числа.

1.	Что такое квадратный корень?
2.	Как найти квадратный корень?
3.	Таблица квадратного корня
4.	Формула квадратного корня
5.	Упрощение квадратного корня
6.	Квадратный корень из отрицательного числа
7.	Квадрат числа
8.	Как найти квадрат числа?
9.	Квадраты и квадратные корни
10.	Часто задаваемые вопросы о квадратном корне

Что такое квадратный корень?

Квадратный корень из числа — это такой множитель числа, который при умножении на себя дает исходное число. Квадраты и квадратные корни являются специальными показателями. Рассмотрим число 9. Когда 3 умножается само на себя, в результате получается 9. Это можно записать как 3 × 3 или 3 ² . Здесь показатель степени равен 2, и мы называем его квадратом. Теперь, когда показатель степени равен 1/2, он относится к квадратному корню из числа. Например, √n = n ^1/2 , где n — целое положительное число.

Квадратный корень Определение

Квадратный корень из числа равен степени 1/2 этого числа. Другими словами, это число, произведение которого само по себе дает исходное число. Он представлен с помощью символа «√». Символ квадратного корня называется радикалом, тогда как число под символом квадратного корня называется радикалом.

Как найти квадратный корень?

Чтобы найти квадратный корень числа, мы просто смотрим, возводя в квадрат, какое число даст фактическое число. Очень легко найти квадратный корень из числа, являющегося полным квадратом. Совершенные квадраты — это положительные числа, которые можно представить как произведение числа самого на себя. Другими словами, совершенные квадраты — это числа, которые выражаются как значение степени 2 любого целого числа. Мы можем использовать четыре метода, чтобы найти квадратный корень из чисел и эти методы следующие:

Метод повторного вычитания
Метод простой факторизации
Метод оценки
Метод длинного деления

Следует отметить, что первые три метода удобно использовать для полных квадратов, а четвертый метод, т.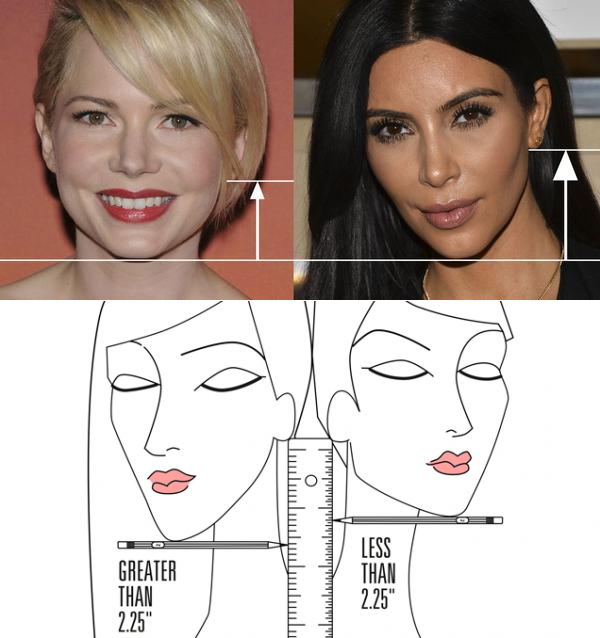 е. метод деления в длину, можно использовать для любого числа, независимо от того, является оно полным квадратом или нет.

Метод многократного вычитания квадратного корня

Это очень простой метод. Мы вычитаем последовательные нечетные числа из числа, для которого мы находим квадратный корень, пока не достигнем 0. Количество раз, которое мы вычитаем, является квадратным корнем данного числа. Этот метод работает только для совершенных квадратных чисел. Найдем квадратный корень из 16, используя этот метод.

16 — 1 = 15
15 — 3 =12
12 — 5 = 7
7- 7 = 0

Вы можете заметить, что мы вычли 4 раза. Таким образом, √16 = 4 ·

Извлечение квадратного корня с помощью метода факторизации простых чисел

Факторизация любого числа простыми числами означает представление этого числа как произведения простых чисел. Чтобы найти квадратный корень данного числа с помощью метода простой факторизации, мы следуем шагам, приведенным ниже:

Шаг 1: Разделите данное число на его простые множители.
Шаг 2: Сформируйте пары факторов так, чтобы оба фактора в каждой паре были равны.
Шаг 3: Возьмите один множитель из пары.
Шаг 4: Найдите произведение множителей, полученных путем взятия одного множителя из каждой пары.
Шаг 5: Этот продукт представляет собой квадратный корень из заданного числа.

Найдем квадратный корень из 144 этим методом.

Этот метод работает, когда заданное число является числом в идеальном квадрате.

Извлечение квадратного корня с помощью метода оценки

Оценка и аппроксимация относятся к обоснованному предположению фактического значения, чтобы сделать расчеты более простыми и реалистичными. Этот метод помогает в оценке и аппроксимации квадратного корня из заданного числа. Воспользуемся этим методом, чтобы найти √15. Найдите ближайшее к 15,9 число в форме идеального квадрата.а 16 — числа с совершенным квадратом, ближайшие к 15. Мы знаем, что √16 = 4 и √9 = 3. Отсюда следует, что √15 лежит между 3 и 4. Теперь нам нужно посмотреть, ближе ли √15 к 3 или 4. Рассмотрим 3,5 и 4. 2 = 16. Таким образом, √15 лежит между 3,5 и 4 и ближе к 4.

Найдем квадраты 3,8 и 3,9. Так как 3,8 ² = 14,44 и 3,9 ² = 15,21. Это означает, что √15 находится между 3,8 и 3,9. Мы можем повторить процесс и проверить между 3,85 и 3,9.. Мы можем заметить, что √15 = 3,872.

Это очень долгий и трудоемкий процесс.

Вычисление квадратного корня методом деления в длину

Деление в длину — это метод деления больших чисел на этапы или части, разбивающий задачу деления на последовательность более простых шагов. С помощью этого метода мы можем найти точный квадратный корень из любого заданного числа. Давайте разберемся с процессом нахождения квадратного корня методом деления в длину на примере. Найдем квадратный корень из 180.

Шаг 1: Поместите черту над каждой парой цифр числа, начиная с разряда единиц (крайняя правая сторона). У нас будет две пары, т.е. 1 и 80
Шаг 2: Мы делим крайнее левое число на наибольшее число, квадрат которого меньше или равен числу в самой левой паре.

Шаг 3: Опустите число под следующей чертой справа от остатка. Прибавьте к делителю последнюю цифру частного. Справа от полученной суммы найдите подходящее число, которое вместе с результатом суммы образует новый делитель для нового делимого, переносимого вниз.

Шаг 4: Новое число в частном будет иметь то же число, которое было выбрано в делителе. Условие то же — либо меньше, либо равно дивиденду.

Шаг 5: Теперь мы продолжим этот процесс дальше, используя десятичную точку и добавляя нули попарно к остатку.

Шаг 6: Полученное частное будет квадратным корнем числа. Здесь квадратный корень из 180 приблизительно равен 13,4 и больше знаков после запятой можно получить, повторив тот же процесс следующим образом.

Таблица квадратного корня

Таблица квадратного корня состоит из чисел и их квадратных корней. Также полезно находить квадраты чисел. Вот список квадратных корней из совершенных квадратных чисел и некоторых несовершенных квадратных чисел от 1 до 10.

Число	Квадратный корень
1	1
2	1.414
3	1,732
4	2
5	2,236
6	2,449
7	2,646
8	2,828
9	3
10	3,162

Числа, не являющиеся полными квадратами, являются иррациональными числами.

Формула квадратного корня

Квадратный корень числа имеет показатель степени 1/2. Формула квадратного корня используется для нахождения квадратного корня из числа. Мы знаем формулу экспоненты: \(\sqrt[\text{n}]{x}\) = x ^1/n . Когда n = 2, мы называем это квадратным корнем. Мы можем использовать любой из вышеперечисленных методов для нахождения квадратного корня, например, разложение на простые множители и так далее. 9^1/2 = √9 = √(3×3) = 3. Итак, формула для записи квадратного корня числа: √x= x ^1/2 .

Упрощение квадратного корня

Чтобы упростить квадратный корень, нам нужно найти простую факторизацию данного числа. Если фактор не имеет пары, сохраните их под символом квадратного корня, в противном случае извлеките одно число из квадратного корня из каждой пары. Например: √12 = \(\sqrt{2 \times 2\times3}\) = 2√3. Это связано с тем, что правило упрощения квадратного корня таково: √xy = √(x × y), где x и y — положительные целые числа.

Для дробей также действует аналогичное правило: √x/√y = √(x/y). Например: √50/√10 = √(50/10)= √5

Квадратный корень из отрицательного числа

Квадратный корень из отрицательного числа не может быть действительным числом, так как квадрат является либо положительным числом, либо нулем. Но у комплексных чисел есть решения квадратного корня из отрицательного числа. Главный квадратный корень -x равен: √(-x)= i√x. Здесь i — квадратный корень из -1.

Например: возьмем квадратное число, например 16. Теперь давайте посмотрим на квадратный корень из -16. Настоящего квадратного корня из -16 не существует. √(-16)= √16 × √(-1) = 4i (как √(-1)= i), где i представлено как квадратный корень из -1. Итак, 4i — это квадратный корень из -16.

Квадрат числа

Любое число, возведенное в степень два (y ² ), называется квадратом основания. Итак, 5 ² или 25 называется квадратом числа 5, а 8 ² или 64 — квадратом числа 8. Мы можем легко найти квадрат числа, умножив число два раза. Например, 5 ² = 5 × 5 = 25 и 8 ² = 8 × 8 = 64. Когда мы находим квадрат целого числа, полученное число представляет собой полный квадрат. Некоторые из идеальных квадратов, которые у нас есть, это 4, 9., 16, 25, 36, 49, 64 и так далее. Квадрат числа всегда положительное число.

☛Также проверьте:

Квадрат от 1 до 50
Квадрат от 1 до 30
Квадрат от 1 до 20
Квадрат от 1 до 25
Квадраты от 1 до 100
Квадрат от 1 до 40

Как найти квадрат числа?

Квадрат числа можно найти, умножив число само на себя. Для однозначных чисел мы можем использовать таблицы умножения, чтобы найти квадрат, а в случае двух или более двузначных чисел мы выполняем умножение числа само по себе, чтобы получить ответ. Например, 9× 9 = 81, где 81 — это квадрат 9. Аналогично, 3 × 3 = 9, где 9 — это квадрат 3.

Квадрат числа записывается путем возведения показателя степени в 2. Например, квадрат 3 записывается как 3 ² и читается как «3 в квадрате». Вот несколько примеров:

4 ² = 4 × 4 = 16
(-6) ² = -6 × -6 = 36
(5/3) ² = 5/3 × 5/3 = 25/9

Квадраты и квадратные корни

Существует очень сильная связь между квадратами и квадратными корнями, поскольку каждый из них является обратным отношением другого. т. е. если x ² = y, то x = √y. Его можно просто запомнить так:

Когда «квадрат» удаляется из одной части уравнения, мы получаем квадратный корень с другой стороны. Например, 4 ² = 16 означает, что 4 = √16. Это также известно как «извлечение квадратного корня с обеих сторон».
Когда «квадратный корень» удаляется из одной части уравнения, мы получаем квадрат с другой стороны. Например, √25 = 5 означает, что 25 = 5·² . Это также известно как «квадрат с обеих сторон»

Эта логика помогает решать многие уравнения в алгебре. Рассмотрим следующий пример:

Пример: Решите уравнение √(2x + 3) = 10.

Решение:

Возведение в квадрат обеих частей уравнения приведет к сокращению квадратного корня в левой части.

2x + 3 = 10 ²

2x + 3 = 100

2x = 97

x = 97/2 = 48,5

Вот еще различия между квадратами и квадратными корнями.

	квадратов	Квадратные корни
Определение	Произведение числа, умноженного само на себя.	Это число, которое при умножении само на себя дает исходное число.
Пример	7 ² = 49	Квадратный корень (√)
Результат	Положительный всегда.	Может быть как положительным, так и отрицательным.
Домен	Набор всех действительных чисел	Набор всех неотрицательных действительных чисел.
Обратный	Обратное значение квадрата равно квадратному корню.	Обратное значение квадратного корня является квадратным.

☛ Статьи по теме

Калькулятор уравнения квадратного корня
Рабочие листы по квадратным корням

Квадратный корень из чисел

Cuemath — одна из ведущих мировых обучающих платформ по математике, предлагающая онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

Часто задаваемые вопросы о квадратном корне

Что такое квадратный корень в математике?

квадратный корень из числа — это число, которое при умножении само на себя дает действительное число. Например, 2 — это квадратный корень 4, и это выражается как √4 = 2. Это означает, что когда 2 умножается на 2, это приводит к 4, и это можно проверить как 2 × 2 = 4.

☛ Проверка:

квадратный корень 1–10239
Квадратный корень от 1 до 20
Квадратный корень от 1 до 25
Квадратный корень от 1 до 30
Квадратный корень от 1 до 50
Квадратный корень от 1 до 100

Как вычислить квадратный корень числа?

Очень легко найти квадратный корень из числа, которое является полным квадратом. Например, 9 — это полный квадрат, 9 = 3 × 3. Итак, 3 — это квадратный корень из 9, и это можно выразить как √9 = 3. Квадратный корень из любого числа, как правило, можно найти, используя любой из четырех методов, приведенных ниже:

Метод повторного вычитания
Метод простой факторизации
Метод оценки и приближения
Метод длинного деления

Может ли квадратный корень быть отрицательным?

Да, квадратный корень из числа может быть отрицательным.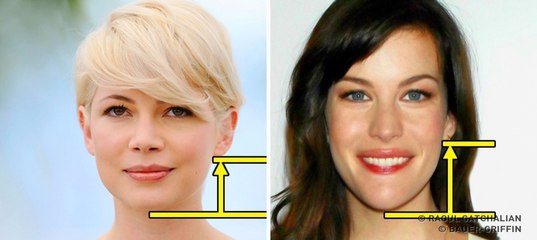 Фактически, все совершенные квадраты, такие как 4, 9, 25, 36 и т. д., имеют два квадратных корня, один из которых является положительным значением, а другой — отрицательным. Например, квадратные корни из 4 равны -2 и 2. Чтобы убедиться в этом, мы можем увидеть, что (-2) × (-2) = 4. Точно так же квадратные корни из 9равны 3 и -3.

Как найти квадратный корень из десятичного числа?

Квадратный корень из десятичного числа можно найти с помощью метода оценки или метода деления в большую сторону. В случае десятичных чисел мы делаем пары целых частей числа и дробных частей отдельно. И затем, мы выполняем процесс деления в длинную точно так же, как и любое другое целое число.

Что такое символ квадратного корня?

Символ, который используется для обозначения квадратного корня, называется подкоренным знаком ‘√ ‘. Термин, написанный внутри подкоренного знака, называется подкоренным.

Как умножить два значения квадратного корня?

Допустим, у нас есть два числа a и b. Сначала найдем квадратный корень из чисел a и b. Затем, после нахождения квадратного корня, мы умножаем значение квадратного корня вместе. Поясним это на практической иллюстрации. Например, умножьте √4 × √16. Квадратный корень из 4 равен 2 (√4 = 2), а квадратный корень из 16 равен 4 (√16 = 4). Теперь мы умножим значение квадратного корня из 4 и 16, т. е. 2 × 4 = 8. Вместо этого мы можем применить свойство квадратных корней, √a × √b = √ab.

Какая формула используется для вычисления квадратного корня из числа?

Квадратный корень из любого числа можно выразить по формуле: √y = y ^½ . Другими словами, если показатель степени числа равен 1/2, это означает, что нам нужно найти квадратный корень из числа.

Что такое квадрат и квадратный корень числа?

Квадрат числа — это произведение, которое получается при умножении числа само на себя. Например, 6 × 6 = 36. Здесь 36 — это квадрат 6. Квадратный корень числа — это множитель числа, и когда он умножается сам на себя, получается исходное число. Теперь, если мы хотим найти квадратный корень из 36, то есть √36, мы получим ответ как √36 = 6. Следовательно, мы можем видеть, что квадрат и квадратный корень числа являются обратными операциями друг друга.

Какой метод используется для нахождения квадратного корня из неполных квадратных чисел?

В математике несовершенным или несовершенным квадратным числом считается число, квадратный корень которого не может быть найден как целое число или как дробь целых чисел. Квадратный корень из несовершенного квадратного числа можно вычислить, используя метод деления в длинную сторону.

Как найти квадратный корень на калькуляторе?

Чтобы найти значение квадратного корня любого числа на калькуляторе, нам просто нужно ввести число, для которого мы хотим получить квадратный корень, а затем вставить символ квадратного корня √ в калькулятор. Например, если нам нужно найти квадратный корень из 81, мы должны ввести 81 в калькулятор, а затем нажать символ √, чтобы получить его квадратный корень. Мы получим √81 = 9.

☛ Проверка:

Калькулятор квадратного корня
Калькулятор квадратного корня дроби
Добавление калькулятора квадратных корней
Калькулятор умножения квадратных корней
Упрощение калькулятора квадратных корней

Каковы применения формулы квадратного корня?

Существуют различные применения формулы квадратного корня:

Формула квадратного корня в основном используется в алгебре и геометрии.
Помогает найти корни квадратного уравнения.
Широко используется инженерами.

Что означает квадрат числа?

Произведение, которое получается при умножении числа само на себя, — это квадрат числа. Например, 5 × 5 = 25. Здесь 25 — это квадрат 5, и это также можно записать как 5 ² = 25.

Как вычислить квадратный корень из отрицательного числа?

Обратите внимание, что квадратный корень из отрицательного числа не является действительным числом.