3. Враг моего врага . Удовольствие от X. Увлекательное путешествие в мир математики от одного из лучших преподавателей в мире
В начальной школе вычитание учат сразу после сложения. И в этом, безусловно, есть смысл: в обоих случаях применяется счет чисел, только при вычитании он выполняется в обратную сторону. Психологически действия тоже похожи: ребенок учится брать и давать примерно в одно и то же время. Сложение и вычитание всегда идут рука об руку. Если человек готов посчитать, сколько будет 23 + 9, то не сомневайтесь, он скоро ответит и на вопрос, сколько будет 23 – 9.
Но если углубиться в эту тему, то в отличие от сложения вычитание создает довольно неприятную проблему, поскольку в результате могут появиться отрицательные числа. Если я захочу взять у вас 6 булочек, а у вас их только 2, то в реальности у меня ничего не получится. Зато в уме я навешу на вас 4 отрицательные булочки, что бы это ни значило.
Вычитание заставляет нас расширить свое представление о числах. Отрицательные числа более абстрактны, чем положительные. Четыре отрицательные булочки не потрогаешь и не съешь, зато их можно представить. Самое интересное, что в реальном мире отрицательные числа тоже встречаются: долги, перерасход по кредитной карте, минусовые температуры зимой и обозначения подвальных уровней на крытых парковках.
Отрицательные числа более абстрактны, чем положительные. Четыре отрицательные булочки не потрогаешь и не съешь, зато их можно представить. Самое интересное, что в реальном мире отрицательные числа тоже встречаются: долги, перерасход по кредитной карте, минусовые температуры зимой и обозначения подвальных уровней на крытых парковках.
Многие из нас пока еще не заключили мир с отрицательными числами. Как заметил мой коллега Энди, люди придумали всевозможные забавные мелкие уловки, чтобы обойти страшный отрицательный знак «минус». В отчетах паевых инвестиционных фондов потери (отрицательные числа) печатаются красным или заключаются в круглые скобки, чтобы минусы ни в коем случае не появились. В исторических книгах сказано, что Юлий Цезарь родился в 100 году до н. э., а не в –100 году. Подземные уровни парковки часто обозначаются как B1 и B2. Температура – одно из немногих исключений, когда люди действительно говорят, что она составляет –5 градусов, хотя и в этом случае многие предпочитают фразу «5 градусов ниже нуля». Видимо, в отрицательном знаке есть нечто отталкивающее и… негативное.
Видимо, в отрицательном знаке есть нечто отталкивающее и… негативное.
Возможно, самое неприятное заключается в том, что при перемножении двух отрицательных чисел получается положительное число. Поэтому позвольте привести доводы в защиту знака минус.
Как нам определить ценность такого выражения, как –1 ? 3, где мы умножаем отрицательное число на положительное? Ну хорошо, так как 1 ? 3 означает сумму 1 + 1 + 1, естественно представить –1 ? 3 как (–1) + (–1) + (–1), что равняется –3. Это должно стать очевидным в примере с деньгами: если вы должны мне 1 доллар в неделю, то по истечении трех недель вы мне будете должны 3 доллара.
Отсюда уже недалеко до понимания, почему минус, умноженный на минус, дает плюс. А теперь взгляните на следующий ряд равенств:
– 1 ? 3 = –3
– 1 ? 2 = –2
– 1 ? 1 = –1
– 1 ? 0 = 0
– 1 ? –1 =?
Посмотрите на числа в правой части равенств и удостоверьтесь в том, что это обычная прогрессия: –3, –2, –1, 0… На каждом шаге мы добавляем 1 к предыдущему числу. Таким образом, разве не логично, что следующим числом будет 1?
Таким образом, разве не логично, что следующим числом будет 1?
Это один аргумент в пользу того, почему (–1) ? (–1) = 1. Привлекательность такого толкования заключается в том, что оно позволяет сохранить правила обычной арифметики – получается, что они верны как для положительных, так и для отрицательных чисел.
Но если вы бесчувственный прагматик, то, вероятно, будете удивлены, что у этих абстракций есть некие параллели в реальном мире. По общему признанию, жизнь иногда играет по различным правилам. В обычных этических построениях два заблуждения не приводят к истине. Более того, двойные отрицания не всегда равнозначны утверждению; они могут усилить отрицание, как в случае с «Я не могу получить никакого удовлетворения». (Действительно, в этом отношении язык может быть очень мудреным. Выдающийся британский философ и лингвист Дж. Остин из Оксфорда как-то в своей лекции заявил, что во многих языках двойное отрицание дает утверждение, но ни в одном дважды повторенное утверждение не дает отрицания. На что сидевший в аудитории философ из Колумбии Сидни Мордженбессер ехидно процедил: «Да-да».)
На что сидевший в аудитории философ из Колумбии Сидни Мордженбессер ехидно процедил: «Да-да».)
Тем не менее есть немало случаев, когда реальный мир действительно отражает правила умножения отрицательных чисел. Например, возбуждение одной нервной клетки может быть подавлено возбуждением второй нервной клетки. Если в этот момент возбуждение второй нервной клетки подавляется третьей нервной клеткой, то первая клетка может снова возбудиться. Косвенное воздействие третьей клетки на первую вызывает ее возбуждение. Таким образом, последовательность двух отрицаний приводит к утверждению. Подобные эффекты происходят и при регуляции генов: белок может включить ген, блокируя другую молекулу, которая подавляла этот отрезок молекулы ДНК.
Возможно, самую понятную параллель можно провести в социально-политической сфере. Как утверждает пословица, «враг моего врага – мой друг». Общеизвестно, что понятия вроде «друг моего врага», «враг моего друга» и тому подобные можно подставить в виде треугольника отношений. {6}
{6}
В углы треугольника помещают людей, компании или страны, а соединяющие их стороны показывают отношения между ними, которые могут быть как позитивными, или дружественными (обычно отображаются сплошными линиями), так и негативными, или враждебными (отображаются пунктирными линиями).
Социологи строят треугольники, подобные треугольнику слева, то есть считая отношения между объектами позитивными, так как разумно любить друзей ваших друзей. Точно так же треугольник справа, с двумя негативными и одной позитивной связью, считается сбалансированным, потому что такая комбинация не вызывает разногласий, даже несмотря на две стороны с негативными связями, поскольку ничто так не цементирует дружбу, как ненависть к одному и тому же человеку.
Конечно, треугольники могут быть выведены из состояния баланса. Это происходит в ситуации, когда есть три врага, причем двое из них относятся друг к другу менее враждебно и готовы объединиться, чтобы напасть на третьего.
Еще менее сбалансированным будет треугольник с единственной негативной связью. Например, предположим, что Кэрол хорошо относится и к Элис, и к Бобу, но Боб и Элис не любят друг друга. Возможно, они когда-то встречались и пережили тяжелое расставание, и теперь говорят друг о друге гадости лояльной к обоим Кэрол. Это создает психологическое напряжение между всеми тремя. Чтобы восстановить баланс, либо Элис и Боб должны урегулировать свои отношения, либо Кэрол должна принять чью-то сторону.
Например, предположим, что Кэрол хорошо относится и к Элис, и к Бобу, но Боб и Элис не любят друг друга. Возможно, они когда-то встречались и пережили тяжелое расставание, и теперь говорят друг о друге гадости лояльной к обоим Кэрол. Это создает психологическое напряжение между всеми тремя. Чтобы восстановить баланс, либо Элис и Боб должны урегулировать свои отношения, либо Кэрол должна принять чью-то сторону.
Во всех этих случаях логика баланса соответствует логике умножения. В сбалансированном треугольнике знак произведения двух любых сторон, положительный или отрицательный, всегда совпадает со знаком третьей стороны. В несбалансированном треугольнике это правило нарушается.
Не будем касаться вопросов о правдоподобии приведенных моделей, ибо здесь возникают интересные вопросы с чисто математическим привкусом. Например, в связной сети, где все друг друга знают, какое самое устойчивое состояние? Прежде всего это нирвана доброжелательности, где все отношения позитивные, а все треугольники в пределах сети сбалансированы. Однако существуют и другие устойчивые состояния. Например, устойчивое к конфликтам состояние, когда сеть раскололась на два враждебных лагеря (произвольных по величине и составу). Все члены одного лагеря хорошо относятся друг к другу, но враждебны к представителям другого лагеря. (Ничего не напоминает?) Возможно, еще более удивительно то, что эти полярные состояния являются единственно возможными столь же устойчивыми состояниями, как нирвана{7}. В частности, ни у какого трехстороннего раскола не может быть уравновешенных треугольников.
Однако существуют и другие устойчивые состояния. Например, устойчивое к конфликтам состояние, когда сеть раскололась на два враждебных лагеря (произвольных по величине и составу). Все члены одного лагеря хорошо относятся друг к другу, но враждебны к представителям другого лагеря. (Ничего не напоминает?) Возможно, еще более удивительно то, что эти полярные состояния являются единственно возможными столь же устойчивыми состояниями, как нирвана{7}. В частности, ни у какого трехстороннего раскола не может быть уравновешенных треугольников.
Ученые использовали этот метод для анализа союзов, сложившихся при подготовке к Первой мировой войне{8}. Диаграммы, представленные ниже, показывают союзы между основными державами, участвовавшими в ней: Великобританией, Францией, Россией, Италией, Германией и Австро-Венгрией между 1872 и 1907 гг.
Первые пять конфигураций были несбалансированными, потому что каждая из них содержала по крайней мере один несбалансированный треугольник. Возникающие в результате разногласия подталкивали эти страны к изменению конфигурации, тем самым вызывая реверберацию в других частях сети. На последнем этапе Европа раскололась на два непримиримых антагонистских блока, придя к общему балансу, но оказавшись на грани войны.
Возникающие в результате разногласия подталкивали эти страны к изменению конфигурации, тем самым вызывая реверберацию в других частях сети. На последнем этапе Европа раскололась на два непримиримых антагонистских блока, придя к общему балансу, но оказавшись на грани войны.
Однако это не значит, что на основании данной теории можно делать прогнозы. Это не так. Подобный подход не позволяет объяснить все тонкости изменений в геополитике. Но некоторые из наблюдаемых нами явлений происходят в соответствии именно с примитивной логикой «враг моего врага» и отлично подпадают под умножение отрицательных чисел. Отделяя важное от незначительного, арифметика отрицательных чисел может помочь нам отыскать настоящие загадки.
Данный текст является ознакомительным фрагментом.
Урок математики в 6-м классе по теме: «Умножение отрицательных чисел»
Цель: Научить умножать
положительные и отрицательные числа, а также
перемножать отрицательные числа.
Ход урока:
1. Устно:
Примеры записаны на карточках, классу
показываю карточки с примерами:
| 4/9 * 1/2 | 0 * 5/6 | 3/7 * 14 | 3 * 1/5 |
| 7/2 * 2/7 | 1/2 * 3/8 | 7 * 4/9 * 1/7 | 5,6 * 1/7 |
| 3/2 * 2/3 | |||
2. Историческая справка:
Индийский математик Брамагупта, живший в VII
веке, пользовался отрицательными числами.
Положительные числа представлял как
“имущества”, Отрицательные числа как “долги”.
Правила сложения положительных и отрицательных
чисел он выражал так:
ПЛАКАТ
| “Сумма двух имуществ — имущество (+
Сумма двух долгов есть долг
(-X)+ (-X)= (-X)”. |
Условившись положительные числа связывать со
словом “друг”, а отрицательные числа со словом
“враг”, древние употребляли интересное правило
умножения:
ПЛАКАТ
| “Друг моего друга — мой друг (+X) * (+X)= (+X)
Друг моего врага — мой враг
(+X) * (-X)= (-X)
Враг моего друга — мой враг
(- X ) * (+ X )= (- X )
Враг моего врага — мой друг
(- X ) * (- X )= (+ X ) |
3. На доске записаны примеры:
(-12) * (-3)=
(-14) * (+5)=
(-14) * (-0,2)=
(-4,2) * 10=
(-6/7) * (-1/2)=
4/21
* (-7/16)=
(-2,4) * (-3)=6
-1,8 * 4=
Ребятам предлагается, используя правила
умножения древних людей вычислить данные
примеры.
Когда примеры решены, прошу учеников попробовать
сформулировать правило умножения двух
отрицательных чисел и правило умножения двух
чисел с разными знаками.
Затем открываем учебник, читаем правила,
сравниваем их с теми, которые мы вывели сами,
делаем вывод, как умножить два отрицательных
числа, как умножить два числа с разными знаками:
1. Надо
указать какое действие.
2. Какие
знаки имеют множители.
3.
Установить знак результата.
4. Найти
модуль произведения.
Рассмотрим № 1105 (а — м) по цепочке с места, с
комментарием.
4. На доске записаны примеры:
а) (-7) * (-5) * 2=
(-4) * (-10) * 8=
б) (-2) * (-3) * (-4)=
(-1,2) * (-2) * (-12)=
в) (-1) * (-2) * (-5) * (-15) * 2=
Надо определить знак произведения и вычислить.
После этого спрашиваю, какой вывод можно сделать
относительно знака произведения, где чётное
(нечётное) число отрицательных множителей?
Если число отрицательных множителей нечетное, то
произведение — число отрицательное.
Если число отрицательных множителей чётное, то
произведение — число положительное.
5.а) Работа с учебником.
№ 1105 (н- т) — двое у
доски
№ 1107 (три ученика у
доски) по одной строчке
5.б) Вычислить: (примеры записаны на доске)
| а) –2,4 * 2 * (-0,5)= | г) 0,2 * (-100) * 3 * 1/3= |
| б) –1/2 * 4/9 * (-27/28) * (-56/57)= | д) 2 * (-3) * 4 * (-5) * 6= |
| в) –9 * 2 * (-3) * 1/2= | е) –2,3 * (-2) * (-8)= |
6. Самостоятельная работа через копировку:
| Вариант 16 | Вариант 2 | ||
| 1) –64 * 10= | (-640) | 1) (-5,8) * 10= | (-58) |
| 2) (-2,8) * 3= | (-8,4) | 2) 82 * (-3)= | (-246) |
| 3) (-4,7) * (-5)= | (23,5) | 3) (-5,4) * (-7)= | (37,8) |
| 4) 6,9 * (-0,1)= | (-0,69) | 4) 1,9 * (-0,1)= | (-0,19) |
| 5) (-6,08) * (-100)= | (608) | 5) (-8,6) * (-100)= | (860) |
| 6) 4/7 * (-7/8)= | (-1/2) | 6) (-3/7) * 7/9= | (-1/3) |
| 7) -4,4 * 5/11= | (-2) | 7) –14/5 * 5/28= | (-1/2) |
| 8) –6,02 * (-3,8)= | (22,876) | 8) –8,06 * (-2,3)= | (18,538) |
| 9) –11/8 * 40/33= | (-5/3) | 9) –13/4 * 40/39= | (-10/3) |
| 10) –8/3 * 9/4= | (-6) | 10) –7/2 * 30/7= | (-15) |
Тетрадь сдаем, “копирку” проверяем, на доске
приведена таблица оценок.
8 — 10 примеров решены верно — оценка “5”
7-6 примеров
— оценка “4”
5-4 примеров
— оценка “3”
Ещё раз повторяем, как умножать два
отрицательных числа, как умножать два числа с
разными знаками.
7. Итоги урока, оценки
Домашнее задание: № 1127, № 1128.
вероятность — % от % — Пожалуйста, помогите мне доказать, что мой друг ошибается
Вот два способа думать о вероятности, которые я часто нахожу полезными.
В частотной интерпретации вероятности у вас есть большое количество ситуаций, устроенных одинаково, и вероятность того, что что-то окажется правдой, говорит вам о доле тех ситуаций, в которых это утверждение верно.
Предположим, есть миллион параллельных вселенных, каждая со своей версией вас, вашего друга, ваших домов и DVD. Тогда заявления вашего друга будут иметь следующие последствия:
Вероятность того, что она у него дома, составляет 30%.
Это означает, что в 30% вселенных, то есть в 300 000 из них, DVD находится в доме вашего друга.
Если DVD находится в его собственном доме, с вероятностью 90% он находится на крыльце и с вероятностью 10% в гостиной.
Позвольте мне разобрать это по частям, потому что это самая важная часть:
Если DVD находится у него дома,
Это означает, что вы должны рассматривать только те вселенные, где DVD находится в доме вашего друга. Их 300 000. Вы должны забыть об остальных вселенных на данный момент.
с вероятностью 90% он на крыльце
В 90% вселенных DVD стоит на крыльце. Но мы притворяемся, что существует всего 300 000 вселенных. Так что в 90% из этих , или 270000 вселенных, DVD стоит на крыльце.
и с вероятностью 10% он в гостиной.
Опять же, мы притворяемся, что всего существует 300 000 вселенных.
 В 10% из этих , или 30000, DVD стоит в гостиной.
В 10% из этих , или 30000, DVD стоит в гостиной.
Хорошо, это все утверждения, так что пора перестать притворяться и вернуться к рассмотрению всех миллионов вселенных. У нас есть следующие итоги:
- 30 000 вселенных, где DVD находится в гостиной в доме вашего друга
- 270 000 вселенных, где DVD лежит на крыльце дома твоего друга
- 700 000 вселенных, где DVD находится в доме его родителей
Чтобы найти вероятность того, что DVD находится на крыльце, вы берете количество вселенных, в которых DVD находится на крыльце, и делите его на общее количество вселенных.
$$P(\text{DVD на крыльце}) = \frac{\text{количество вселенных, где он находится на крыльце}}{\text{общее количество вселенных}} = \frac{270\,000} {1\,000\,000} = 27%$$
И аналогично для остальных случаев:
$$\begin{align}
P(\text{DVD в гостиной}) \\
&= \frac{\text{количество вселенных, если оно находится в гостиной}}{\text{общее количество вселенных}} \\
&= \frac{30\,000}{1\,000\,000} \\
&= 3\%
\end{выравнивание}$$
а также
$$\begin{выравнивание}
P(\text{DVD в доме родителей})
&= \frac{\text{количество вселенных, где он находится в доме его родителей}}{\text{общее количество вселенных}} \\
&= \frac{700\,000}{1\,000\,000} \\
&= 70\%
\end{выравнивание}$$
Вы также можете комбинировать дела:
$$\begin{выравнивание}
P(\text{DVD в гостях у друга})
&= \frac{\text{количество вселенных, где оно находится в доме вашего друга}}{\text{общее количество вселенных}} \\
&= \frac{30\,000 + 270\,000}{1\,000\,000} \\
&= 30\%
\end{выравнивание}$$
что было предположением с самого начала, так что, конечно, будет результатом , но приятно видеть, что математика работает.
Если вы попытались сказать
Если есть три места, где он может быть, то вероятность того, что он на крыльце, составляет 33,333%.
, тогда вы будете утверждать, что в 333 333 вселенных DVD стоит на крыльце. Это явно противоречит нашим подсчетам, что DVD находится на крыльце только в 270 000 вселенных! Таким образом, если более ранние утверждения о вероятности (30%, что это в его доме и т. д.) верны, это последнее утверждение также не может быть правильным. Вы не можете предположить, что вероятность того, что что-то окажется правдой, равна $1/N$ только потому, что существует $N$ возможностей! Нет, если вы каким-то образом не знаете, что все возможности равновероятны. (На самом деле я не говорил этого раньше, но когда я изобрел миллион вселенных, я предположил , что все вселенные равновероятны. Это важно.)
В байесовской интерпретации вероятность является отражением того, как много вы знаете или не знаете о той или иной системе. Поначалу это кажется очень похожим на частотную интерпретацию, но работает немного по-другому, когда вы начинаете говорить о условных вероятностях («если X, то вероятность Y равна Z»).
Поначалу это кажется очень похожим на частотную интерпретацию, но работает немного по-другому, когда вы начинаете говорить о условных вероятностях («если X, то вероятность Y равна Z»).
Чтобы объяснить это, позвольте мне вернуться к вселенным. Мы начали с миллиона из них. Тогда вы сказали
Вероятность того, что она у него дома 30%
, что означает, что 300 000 вселенных имеют DVD в доме вашего друга. Хорошо, это то же самое, что и частотная интерпретация.
Затем переходите к следующему утверждению, и снова я буду разбирать его по частям:
Если DVD находится у него дома,
Хорошо, теперь мы говорим вы определили, что DVD — это в доме вашего друга . Именно здесь байесовская интерпретация отличается от частотной интерпретации: в остальной части этого утверждения мы будем говорить, что вы знаете , что DVD находится в доме вашего друга.
 Таким образом, вы можете буквально отбросить 700 000 вселенных, где это не так. Их больше не существует.
Таким образом, вы можете буквально отбросить 700 000 вселенных, где это не так. Их больше не существует.Как я уже сказал, это довольно тонкая разница.
Одним из следствий этого, кстати, является то, что вероятность того, что DVD находится в доме вашего друга, теперь равна 100%. Или, если быть более точным, когда вы узнали, что DVD находится в доме вашего друга, вы обновили вероятность того, что DVD находится в доме вашего друга, с 30 % (это 300 000/1 000 000) до 100 % (это 300 000/300 000).
с вероятностью 90% он на крыльце
В 90% вселенных DVD стоит на крыльце. Существует 300 000 вселенных, поэтому в 90% из них, или в 270 000 вселенных, DVD лежит на крыльце.
и с вероятностью 10% он в гостиной.
В 10% из 300 000 вселенных или в 30 000 из них DVD находится в гостиной.
Если вы теперь вернетесь к моменту, когда вы не знали, что DVD был в доме вашего друга, вы увидите, что вероятности оказываются такими же, как и в частотной интерпретации. (В целом это верно. Эти интерпретации — просто разные способы осмысления вероятности, но они приводят к одним и тем же результатам.)
(В целом это верно. Эти интерпретации — просто разные способы осмысления вероятности, но они приводят к одним и тем же результатам.)
Существуют математические процедуры для «обратного» предположения, которое вы сделали, но я не буду вдаваться в подробности. Дело в том, что байесовская вероятность является отражением ваших знаний о системе, и вы обновляете вероятности по мере того, как узнаете о ней больше.
логика — А и В враги, В и С враги, какая связь между А и С?
$\begingroup$
Предположим, отношения между любой парой из A, B, C являются либо друзьями, либо врагами.
Вопрос:
Если А и В враги, В и С враги, то каковы отношения между А и С? Они враги или друзья? как выразить такие вопросы, используя математические символы, чтобы было легче думать?
Легко понять, что если A, B друзья, B, C друзья, то A, C тоже друзья.
$\endgroup$
14
$\begingroup$
Я полагаю, используемые символы зависят от того, что вы хотите определить.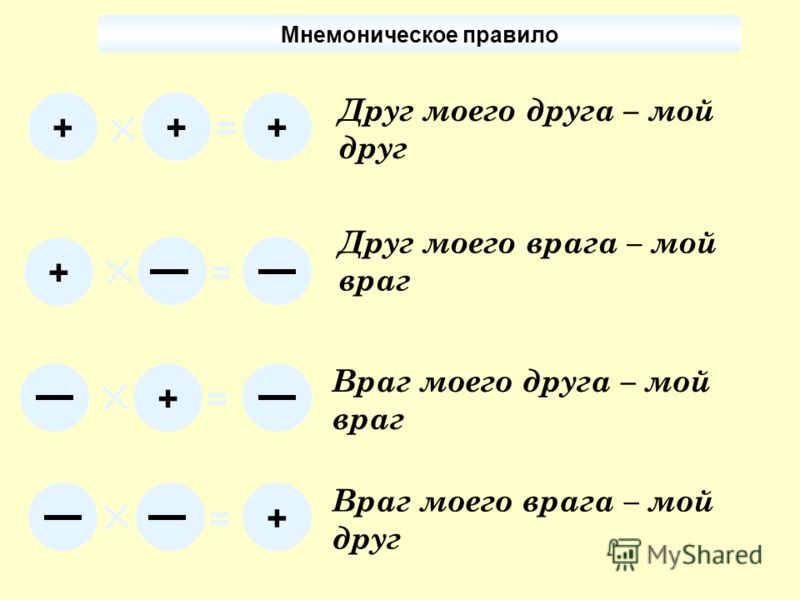 Если я определяю это отношение как отношение эквивалентности, то $X$ и $Y$ являются друзьями тогда и только тогда, когда $X \equiv Y$. Но отношения эквивалентности транзитивны, и тогда $X \equiv Y \wedge Y \equiv Z \Rightarrow X \equiv Z $.
Если я определяю это отношение как отношение эквивалентности, то $X$ и $Y$ являются друзьями тогда и только тогда, когда $X \equiv Y$. Но отношения эквивалентности транзитивны, и тогда $X \equiv Y \wedge Y \equiv Z \Rightarrow X \equiv Z $.
Значит, друг моего друга будет моим другом.
Но таким образом я заставил дружбу быть транзитивной, потому что я предположил, что это отношение эквивалентности .
Обратите внимание, однако, что $X \not\equiv Y \wedge Y \not\equiv Z $ ничего не говорит об отношении между $X $ и $Z $.
Тем не менее, в реальном мире дружба не транзитивна, как указано в комментариях. На самом деле, я не очень люблю лучшего друга моего лучшего друга.
$\endgroup$
2
$\begingroup$
Я придумал аналогию, которая, как мне кажется, очень интуитивна: предположим, что если у двух людей любимый цвет одинаков, то они друзья; иначе они враги.


 В 10% из этих , или 30000, DVD стоит в гостиной.
В 10% из этих , или 30000, DVD стоит в гостиной. Таким образом, вы можете буквально отбросить 700 000 вселенных, где это не так. Их больше не существует.
Таким образом, вы можете буквально отбросить 700 000 вселенных, где это не так. Их больше не существует.