Математические трюки на все случаи жизни: как решить любую задачу
Как бы мы не говорили, что математика особо не нужна в жизни, мы все пользуемся ей постоянно. А эти простые трюки могут облегчить решение любых повседневных математических задач.
Getty Images
Простые математические действия, такие как умножение и деление, зачастую отнимают у нас много умственных сил и времени. Вот как их упростить
Математика может быть кошмарным предметом для большинства людей, особенно для некоторых студентов. Тем не менее, без нее в нашем мире никуда — так или иначе нам приходится как минимум часто делить, умножать, вычитать и складывать. И не всегда под рукой будет калькулятор, чтобы совершить эти действия. Вот несколько трюков, которые позволят совершать все эти действия в уме очень просто.
Умножить на 9 при помощи пальцев
Давайте вычислим, чем равно 9 X 8, используя наши пальцы, чтобы увидеть, как это работает.
- Вытяните руки ладонями вверх.
 Затем пронумеруйте каждый из ваших 10 пальцев, начиная с 1 до 10 и двигаясь от большого пальца левой руки к большому пальцу правой.
Затем пронумеруйте каждый из ваших 10 пальцев, начиная с 1 до 10 и двигаясь от большого пальца левой руки к большому пальцу правой. - Согните палец, который вы хотите умножить на 9, в нашем случае это 8—й палец — средний палец на правой руке.
- Сосчитайте пальцы слева направо до согнутого — в этом случае у вас получится 7 (десятки). Затем сосчитайте пальцы, после согнутого пальца, и получите 2 (единицы). Ответ 72.
Умножение числа на 7
Давайте попробуем умножить 7 X 8 так же при помощи пальцев:
- Держите руки ладонями к себе, так, чтобы пальцы были обращены друг к другу. Перечислите свои пальцы, начиная с 6 по 10, убедившись, что ваши мизинцы равны 6, безымянные пальцы равны 7, а остальные идут в порядке возрастания до большого пальца, которому должно соответствовать число 10.
- Помните, что ваши пальцы левой руки представляют число слева от задачи, в то время как пальцы правой руки предназначены для чисел с правой стороны. Выстройте их так, чтобы ваш левый безымянный палец (7) касался вашего правого среднего пальца (8).

- Умножая верхние пальцы на левой руке на верхние пальцы на правой руке, вы получаете 3 X 2 = 6 — вы нашли второе число (единицы) вашего окончательного ответа. Теперь у вас есть 5 пальцев под ними, представляющих десятки. Умножьте 5 на 10 и суммируйте его с ранее найденным числом, в нашем случае это 50 + 6 = 56. Вуаля!
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Умножение числа на 3
Похожий метод можно использовать для умножения числа на 3:
- Вытяните одну из ваших рук и назначьте 3 числа каждому из ваших пальцев. Таким образом, на вашем мизинце будет 1, 2, 3, а на безымянном пальце — 4, 5, 6 и т.д. Повторяйте, пока не присвоите 13, 14 и 15 своему большому пальцу. Вы также можете начать присваивать числа, начиная с большого пальца, а не с мизинца.
- Теперь, когда мы вычисляем 3 X 4, поднимите только 4 пальца, а остальные закройте.
- Наконец, сосчитайте все числа на 4 пальцах — ответ 12.
Как быстро найти квадрат числа
В математике нечетное число — это число, которое оставляет 1 в качестве остатка при делении на 2, например, 1, 3, 5, 7 и т. д. Удивительно, но когда вы суммируете последовательные нечетные числа (начиная с 1), вы получаете квадрат числа, соответствующего количеству нечетных цифр в последовательности. Например, сложив последовательно пять нечетных цифр (1+3+5+7+9), вы получите квадрат 5 (25).
д. Удивительно, но когда вы суммируете последовательные нечетные числа (начиная с 1), вы получаете квадрат числа, соответствующего количеству нечетных цифр в последовательности. Например, сложив последовательно пять нечетных цифр (1+3+5+7+9), вы получите квадрат 5 (25).
Быстро умножить число на 999
Если вы умножаете на одну цифру, например, 6 X 999, выполните этот трюк:
- Сначала у нас есть три 9 — мы берем одну из них и умножаем ее на шесть, 6 х 9, и получаем 54. Затем запишите 5 и 4, оставив между ними пространство.
- У нас все еще есть две цифры 9, и мы записываем их между 5 и 4. Ответ 5994.
Если число, на которое вы умножаете, состоит из 3 цифр, например, 255 X 999, то выполните следующие действия:
- Сначала вычтите 1 из 255, и вы получите 254.
- Затем возьмите 9 слева, ближе всего к 255. Вычтите из нее первую цифру вашего трехзначного числа. Получается, 9-2 = 7
- Повторите аналогичный путь для остальных 9.
 Таким образом, возьмите среднее число 9 и вычтите 5, это 9-5 = 4. Наконец, возьмите 9 в правом конце, вычтите 4 и найдите 9-4 = 5.
Таким образом, возьмите среднее число 9 и вычтите 5, это 9-5 = 4. Наконец, возьмите 9 в правом конце, вычтите 4 и найдите 9-4 = 5. - Поставьте последовательно в ряд сначала число из пункта 1, а затем все три числа, которые получились в последующих пунктах. Ответ готов!
Ответ 254745.
«Математические трюки для быстрого счета»
Фанат математики и научный журналист Ингве Фогт с детства увлекался числами и счетом. В книге «Математические трюки для быстрого счёта» (издательство «Альпина нон-фикшн»), переведенной на русский язык Анастасией Наумовой, Фогт собрал интересные способы быстро решать арифметические задачи. От читателя не требуется ничего, кроме знания базовых правил арифметики. N + 1 предлагает ознакомиться с отрывком, посвященным методу скоростного счета в уме, который был придуман бежавшим из России инженером и математиком Яковом Трахтенбергом.
Супербыстрый
швейцарский метод сложения
Я никогда не забуду ту радость, с которой получил от отца в подарок волшебную книгу Микаэля Шрёдера «Молниеносный счет в уме» (Lynregning). Мне было 14 лет, я все детство мечтал о волшебной книге, способной научить меня считать в уме, и теперь даже задрожал от восторга. Передо мной лежала книга, где рассказывалось о таких приемах, о которых я и не подозревал. Помимо прочего, там говорилось о способе складывать огромные числа без особого труда. Если в совершенстве овладеть этим способом, складывать числа можно намного быстрее и веселее, чем если пользоваться классическим школьным приемом.
Мне было 14 лет, я все детство мечтал о волшебной книге, способной научить меня считать в уме, и теперь даже задрожал от восторга. Передо мной лежала книга, где рассказывалось о таких приемах, о которых я и не подозревал. Помимо прочего, там говорилось о способе складывать огромные числа без особого труда. Если в совершенстве овладеть этим способом, складывать числа можно намного быстрее и веселее, чем если пользоваться классическим школьным приемом.
Этот новый метод сложения был изобретен беженцем из России, которому лишь благодаря чуду удалось выжить в нацистском концлагере и добраться до Швейцарии. Бедный, как церковная крыса, Трахтенберг всего за несколько лет успел усовершенствовать методы расчетов, использовавшиеся в швейцарских банках. Яков Трахтенберг с детства имел склонность к математике. Он родился в 1888 г. в Одессе, в обеспеченной семье. В 1912-м Трахтенберг получил должность главного инженера на Обуховском заводе в Санкт-Петербурге, где строились военные суда для российского флота. В 1917-м к власти в России пришли коммунисты. Трахтенберг, убежденный пацифист, обрадовался, узнав, что теперь завод будет выпускать тракторы. Но спустя некоторое время Трахтенберга обвинили в пособничестве царскому режиму. Ему чудом удалось спастись: переодевшись крестьянином, он бежал из страны. В 1919 г. Яков приехал в Берлин и начал жизнь с чистого листа.
В 1917-м к власти в России пришли коммунисты. Трахтенберг, убежденный пацифист, обрадовался, узнав, что теперь завод будет выпускать тракторы. Но спустя некоторое время Трахтенберга обвинили в пособничестве царскому режиму. Ему чудом удалось спастись: переодевшись крестьянином, он бежал из страны. В 1919 г. Яков приехал в Берлин и начал жизнь с чистого листа.
Через несколько лет он женился на еврейской девушке, но с приходом к власти Гитлера им пришлось бежать в Австрию. Здесь Яков Трахтенберг написал труд под названием «Министерство мира» — своего рода пародию на гитлеровскую автобиографию «Моя борьба», где высмеивал фюрера и его боевых соратников. Австрийские нацисты почувствовали себя невероятно оскорбленными. В 1938 г. за день до захвата нацистской Германией Австрии Трахтенберга арестовали. Он смог сбежать и добраться до Югославии, но его опять схватили и отправили в концентрационный лагерь Заксенхаузен. Чтобы не сломаться и сохранить рассудок, Трахтенберг, несмотря на постоянные пытки и допросы, придумывал новые методы счета. Он отрывал кусочки ногтей и выскребал ими примеры на стенах барака. Его целью было разработать новую систему счисления.
Он отрывал кусочки ногтей и выскребал ими примеры на стенах барака. Его целью было разработать новую систему счисления.
В конце войны его жена раздобыла фальшивые документы и добилась перевода Якова Трахтенберга в трудовой лагерь, расположенный в Южной Германии. Оттуда они вдвоем сбежали в Швейцарию. С момента злополучного ареста в Австрии прошло семь лет. Якову Трахтенбергу вновь пришлось начинать жизнь с чистого листа. Ему хотелось поделиться своими идеями о быстром счете с другими, однако они никого не интересовали, пока Трахтенберг не стал обучать математике сына местного полицмейстера. Мальчик, сперва совершенно безнадежный, после занятия с Трахтенбергом научился умножать огромные числа на 11. За несколько лет тысячи швейцарцев освоили новый метод счета, придуманный Трахтенбергом. Этот метод приобрел такую популярность, что математик основал собственный институт, где занимались счетом в уме. И первым преподавателем в этом институте стал — кто бы вы думали? Сын полицмейстера!
Один из многих методов Трахтенберга позволяет складывать множество многозначных чисел всего за несколько секунд, проверять верность полученного ответа и, что немаловажно, находить столбец, в котором прячется ошибка, если таковая имеется.
Давайте проверим метод Трахтенберга и сложим следующие числа:
Используя классический школьный метод сложения, мы, скорее всего, сначала сложили бы числа в правом столбце (4 + 7 + 8 + 9 + 8 + 5 = 41), после чего приступили бы к следу ющим столбцам. С сегодняшнего дня и с этого самого момента вам достаточно будет складывать числа только до 11. Иначе говоря, с бо́льшими числами мы вообще не будем иметь дела. Первое правило — выделим число 11. Каждый раз, досчитав до 11, сделаем отметку, вычтем одиннадцать из имеющейся суммы и продолжим.
Для начала посмотрим на правый столбец.
4 + 7 = 11. Сделаем отметку, вычтем 11 и продолжим.
8 + 9 = 17. Здесь тоже есть 11, и еще остается 6.
6 + 8 = 14. Снова 11, и еще осталось 3.
3 + 5 = 8.
Мы выделили три раза по 11, и еще в правом столбце у нас осталось 8. Запишем два этих важных числа друг под другом. Остаток, то есть 8, запишем в одной строке, а количество чисел 11 — в другой.
Проделаем то же самое с другими столбцами. Решайте сами, хотите ли двигаться слева направо или в противоположном направлении. От порядка действий ничего не зависит. Если хотите, можете сперва подсчитать количество чисел 11 во всех столбцах. Все зависит от вашего желания. Единственное, о чем необходимо помнить, — это делать отметку каждый раз, когда сумма составит 11.
Решайте сами, хотите ли двигаться слева направо или в противоположном направлении. От порядка действий ничего не зависит. Если хотите, можете сперва подсчитать количество чисел 11 во всех столбцах. Все зависит от вашего желания. Единственное, о чем необходимо помнить, — это делать отметку каждый раз, когда сумма составит 11.
У нас появилось две новых строки. В верхней — количество единиц, а в нижней — количество чисел 11 в каждом столбце. Эти числа, единицы и одиннадцатки, нужно сложить определенным образом.
Фокус в том, чтобы записать вычисления в виде буквы L. Это означает, что в каждом столбце мы не только складываем единицы и одиннадцатки, но также учитываем количество чисел 11 в правом столбце. И, пожалуйста, не забывайте про числа в уме.
(Складываем 8 и 3 — получаем 11. Записываем число 1 и держим 1 в уме.)
(Складываем 4, 2, 3 и 1 (в уме) — получаем 10. Записываем число 0 и держим 1 в уме.)
(Складываем 5, 3, 2 и 1 (в уме) — получаем 11. Записываем число 1 и держим 1 в уме. )
)
(Складываем 9, 1, 3 и 1 (в уме) — получаем 14. Записываем число 4 и держим 1 в уме.)
(Складываем 1 и 1 (в уме) — получаем 2.)
Возможно, кому-то покажется, что такие расчеты занимают столько же времени, сколько традиционный метод, но, когда метод Трахтенберга внедрили в швейцарских банках, скорость работы существенно возросла. Может, вовсе не удивительно, что Швейцария получила мировую известность благодаря своим банкам?
Основные преимущества нового метода заключаются в том, что с ним, во-первых, проще проверить правильность ответа, а во-вторых, понять, в каком столбце кроется ошибка. Следовательно, если вам не повезло и вы ошиблись, вовсе не обязательно считать все заново. Вместо этого вы сразу можете перейти к столбцу с ошибкой. Чтобы найти ошибку, надо сперва вычислить общую сумму чисел в каждом столбце. Как вы, возможно, помните, вычисляя общую сумму, можно выбросить все девятки.
Начнем с общей суммы чисел в правом столбце. Здесь у нас числа 4, 7, 8, 9, 8 и 5.
4 + 7 = 11. Общая сумма цифр в числе 11 равна 2.
2 + 8 = 10. Сумма цифр в числе 10 составляет 1.
1 + 8 = 9. Не забываем выбрасывать девятки. Тогда у нас остается 5.
Сокращенная сумма цифр во втором столбце справа будет следующей: 5 + 3 + 3 = 11. Сумма цифр в числе 11 равна 2. Следовательно, 2 + 1 + 5 = 8. Последняя цифра у нас 9. Ее можно отбросить. Сокращенная сумма цифр в этом столбце составляет 8. Сокращенная сумма цифр во всех четырех столбцах составляет:
2 2 8 5
Это называется контрольным числом для всех четырех столбцов. Главное — найти взаимосвязь между числами 1, 11 и теми, что у нас в столбцах. Наслаждайтесь моментом, потому что это настоящее волшебство метода Трахтенберга. Контрольные числа каждого столбца должны совпадать с сокращенной суммой единиц и удвоенных одиннадцаток.
9 5 4 8 (единицы)
1 3 2 3 (одиннадцатки)
2 2 8 5 (контрольные числа)
Пойдем справа.
8 + 3 + 3 = 14. Сумма цифр в числе 14 составляет 5. Этот же ответ мы получили, когда вычислили контрольное число для правого столбца.
4 + 2 + 2 = 8. Сокращенная сумма цифр во всем столбце тоже составляет 8.
5 + 3 + 3 = 11. Сумма цифр в числе 11 составляет 2. Значит, все верно.
9 + 1 + 1 = 11. Сумма цифр в числе 11 составляет 2. Значит, тут тоже все правильно.
Если бы в расчетах была ошибка, мы бы сразу же увидели, в каком она столбце. Вместо того чтобы складывать числа во всех столбцах заново, нам достаточно заново пересчитать лишь один столбец. Это позволяет здорово сэкономить время! Неудивительно, что метод Трахтенберга завоевал в свое время такую популярность, ведь тогда калькуляторы и счетные машинки еще не уничтожили необходимость считать в уме. Однако, если бы все владели методом Трахтенберга, стать чемпионом быстрого счета было бы непросто. Поэтому лучше придумать секретные правила, о которых никто больше не знает.
Подробнее читайте:
Фогт И. Математические трюки для быстрого счёта / Ингве Фогт ; Пер. с норв. [Анастасии Наумовой] — М.: Альпина Паблишер, 2020. — 183 с.
15 математических трюков для детей
Содержание
| 1. | Введение |
| 2. | 15 математических трюков для детей |
| 3. | Заключение |
| 4. | О Куэмате |
| 5. | Внешние ссылки |
18 января 2021 г.
Время чтения: 6 минут
Введение
Не все умеют жонглировать числами, но эта тема не так сложна, как кажется, если использовать простые математические приемы, которые помогут решить любую задачу. задача по математике проще простого!
Чтобы легко понять математику, этот предмет можно рассматривать как игру со строительными блоками, наложенными друг на друга — база должна иметь прочную основу для перехода к более сложным концепциям и сложным приложениям.
Многих учеников, а также родителей пугают математические задачи, особенно если они связаны с большими числами и сложными вычислениями.
Математические трюки помогут вам освоить приемы быстрого решения вопросов и могут помочь учащимся развить уверенность в математике, улучшить математические навыки и понимание.
15 математических трюков, которые поразят вас-PDF
Вот несколько простых математических трюков, которые помогут вам выполнять вычисления быстрее и проще. Математические трюки помогут вам освоить методы быстрого решения вопросов и могут помочь учащимся развить уверенность в математике. Вот загружаемый PDF-файл, чтобы узнать больше.
| 📥 | 15 математических трюков, которые взорвут ваш мозг-PDF | Скачать |
Также важно учитывать, как взаимосвязаны понятия математики. То, что вы узнали об умножении, можно применить к делению, что также относится к множителям и множителям, которые можно использовать для понимания дробей. Математические приемы помогают найти такие связи между понятиями и ускорить расчеты.
То, что вы узнали об умножении, можно применить к делению, что также относится к множителям и множителям, которые можно использовать для понимания дробей. Математические приемы помогают найти такие связи между понятиями и ускорить расчеты.
Математические приемы, выученные в раннем возрасте, работают как по волшебству и помогают учащимся преуспеть в учебе, а курсы повышения квалификации открывают множество возможностей для будущего.
Читайте также:
- Трюки сложения и вычитания
- Приемы возведения в квадрат и квадратного корня
- Трюки с умножением и делением
- Хитрости и важность ведической математики
- Попробуйте некоторые умопомрачительные математические фокусы!
15 математических трюков для детей
1. Умножение на 6
Если умножить 6 на четное число, ответ будет заканчиваться той же цифрой. Число в разряде десятков будет составлять половину числа в разряде единиц. Эта уловка работает без особых усилий, и ученики могут добавить ее в свою коллекцию математических фокусов!
Эта уловка работает без особых усилий, и ученики могут добавить ее в свою коллекцию математических фокусов!
| Пример |
6 х 4 = 24
2. Ответ равен 2
Задумайте число.
Умножьте это на 3.
Добавить 6.
Разделите это число на 3.
Вычтите число из шага 1 из ответа на шаге 4.
Ответ: 2.
3. Одно и то же трехзначное число
Задумайте любое трехзначное число, в котором все цифры одинаковы. Примеры включают 333, 666, 777 и 999.
Сложите цифры.
Разделите трехзначное число на ответ в шаге 2.
Ответ: 37.
4. Шесть цифр становятся тремя
Возьмите любое трехзначное число и запишите его дважды, чтобы получилось шестизначное число. Примеры включают 371371 или 552552.
Разделите число на 7.
Разделите его на 11.
Разделите его на 13.
Порядок, в котором вы делаете деление, не имеет значения!
Ответ — трехзначное число.
| Пример |
371371 дает вам 371 или 552552 дает вам 552.
Связанный трюк состоит в том, чтобы взять любое трехзначное число.
Умножьте его на 7, 11 и 13. 90 134
В результате получится шестизначное число, которое повторяет трехзначное число.
| 456 становится 456456 |
5. Правило 11
Правило 11 — это один из тех фокусов и методов, которые можно использовать для быстрого умножения двузначных чисел на 11 в уме.
Разделите две цифры в уме.
Сложите две цифры вместе.
Поместите число из шага 2 между двумя цифрами. Если число из шага 2 больше 9, поместите цифру единиц в пробел и перенесите цифру десятков.
| Пример |
72 х 11 = 792.
57 x 11 = 5 _ 7, но 5 + 7 = 12, поэтому поставьте 2 в пробел и прибавьте 1 к 5, чтобы получить 627
6. Запоминание числа Пи
Это, наверное, самый забавный математический трюк: чтобы запомнить первые семь цифр числа пи, посчитайте количество букв в каждом слове предложения:
«Как бы я хотел, чтобы я мог вычислить число пи».
Это становится 3.141592.
| 3.141592 |
7. Содержит цифры 1, 2, 4, 5, 7, 8
Выберите число от 1 до 6.
Умножьте число на 9.
Умножьте это на 111.
Умножьте это на 1001.
Разделите ответ на 7.
Номер будет содержать цифры 1, 2, 4, 5, 7 и 8.
| Пример |
Число 6 дает ответ 714285.
| 714285 |
8. Умножение больших чисел в уме
Еще один математический фокус и метод, который можно применить для легкого умножения двух двузначных чисел, заключается в использовании их расстояния от 100 для упрощения математики:
Вычтите каждое число из 100.
Сложите эти значения вместе.
100 минус это число — первая часть ответа.
Умножьте цифры из шага 1, чтобы получить вторую часть ответа.
9. Суперпростые правила делимости
У вас есть 210 кусков пиццы, и вы хотите знать, сможете ли вы разделить их поровну в своей группе. Вместо того, чтобы доставать калькулятор, используйте эти простые сочетания клавиш, чтобы посчитать в уме:
Делится на 2, если последняя цифра кратна 2 (210).
Делится на 3, если сумма цифр делится на 3 (522, потому что цифры в сумме дают 9, что делится на 3).
Делится на 4, если последние две цифры делятся на 4 (2540, потому что 40 делится на 4).
Делится на 5, если последняя цифра 0 или 5 (9905).
Делится на 6, если соответствует правилам как для 2, так и для 3 (408).
Делится на 9, если сумма цифр делится на 9(6390, так как 6 + 3 + 9 + 0 = 18, что делится на 9).
Делится на 10, если число оканчивается на 0 (8910).
Делится на 12, если применяются правила делимости на 3 и 4.
| Пример |
210 кусочков пиццы можно равномерно распределить на группы по 2, 3, 6, 10 штук. Вы поняли, что можете использовать их для умножения? Простой математический трюк, чтобы сделать «9» таблица умножения заключается в том, чтобы положить обе руки перед собой с вытянутыми пальцами. Чтобы умножить 9 на число, сложите этот палец вниз, считая слева.
| Пример 1 |
Чтобы умножить 9 на 5, согните безымянный палец слева. Сосчитайте пальцы по обе стороны от «сгиба», чтобы получить ответ. В этом случае ответ равен 45.
Сосчитайте пальцы по обе стороны от «сгиба», чтобы получить ответ. В этом случае ответ равен 45.
| Пример 2 |
Чтобы умножить 9 на 6, отогните шестой палец, что даст результат 54.
11. Сложение больших чисел
Сложение больших чисел только в уме может быть трудным. Этот метод показывает, как упростить этот процесс, сделав все числа кратными 10. Вот пример:
.
644 + 238
Хотя с этими цифрами трудно спорить, округление сделает их более управляемыми. Итак, 644 становится 650, а 238 становится 240.
Теперь сложите 650 и 240 вместе. Итого 890. Чтобы найти ответ на исходное уравнение, нужно определить, сколько мы прибавили к числам, чтобы округлить их.
650 – 644 = 6 и 240 – 238 = 2
Теперь сложите 6 и 2 вместе, чтобы получить 8
.
Чтобы найти ответ на исходное уравнение, из 890 нужно вычесть 8.
890 – 8 = 882
Таким образом, ответ на 644 +238 равен 882.
12. Вычитание из 1000
Вот основное правило для вычитания большого числа из 1000: вычтите каждое число, кроме последнего, из 9 и вычтите последнее число из 10
Например:
1000 – 556
Шаг 1: вычтите 5 из 9 = 4
.
Шаг 2: вычтите 5 из 9 = 4
.
Шаг 3: Вычтите 6 из 10 = 4
.
Ответ: 444.
13. Умножение любого числа в 5 раз
При умножении числа 5 на четное число есть быстрый способ найти ответ.
| Пример 1 |
Например, 5 х 4 =
Шаг 1: Возьмите число, умноженное на 5, и разделите его пополам, чтобы число 4 стало числом 2.
Шаг 2: Добавьте ноль к числу, чтобы найти ответ. В этом случае ответ равен 20.
5 x 4 = 20
| Пример 2 |
При умножении нечетного числа на 5 формула немного отличается.
Например, рассмотрим 5 x 3.
Шаг 1: Вычтите единицу из числа, умноженного на 5, в этом случае число 3 становится числом 2.
Шаг 2: Теперь разделите число 2 пополам, что сделает его числом 1. Сделайте 5 последней цифрой. Полученное число равно 15, что и является ответом.
5 x 3 = 15
14. Уловки с делением
Вот простой математический трюк, позволяющий узнать, можно ли разделить число без остатка на эти определенные числа:
10, если число заканчивается на 0
9, когда цифры складываются вместе и сумма делится на 9 без остатка
8, если последние три цифры делятся на 8 без остатка или равны 000
6, если это четное число, и когда цифры складываются вместе, ответ делится на 3 без остатка
5, если он заканчивается на 0 или 5
4, если он заканчивается на 00 или двузначное число, которое делится без остатка на 4
3, когда цифры складываются вместе и результат делится без остатка на число 3
2, если он заканчивается на 0, 2, 4, 6 или 8
15. Трудное умножение
Трудное умножение
При умножении больших чисел, если одно из чисел четное, разделите первое число пополам, а затем удвойте второе число. Этот метод быстро решит проблему.
| Пример |
Например, рассмотрим 20 x 120
Шаг 1: Разделите 20 на 2, что равно 10. Удвойте 120, что равно 240.
Затем перемножьте два ваших ответа.
10 х 240 = 2400
Ответ на 20 х 120 — 2400.
Заключение
Математические трюки — отличный способ развлечься! Ваш ребенок сможет делать сложные вычисления без помощи калькулятора, используя свои умственные способности.
При регулярной практике учащиеся быстро освоят эти математические трюки в уме, чтобы быстро считать. Математические трюки чрезвычайно поучительны и сделают ваших детей невероятно уверенными в числах, как никогда раньше!
О Cuemath
Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-классы для ученых и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей, чтобы развить несколько навыков. Ознакомьтесь со структурой Cuemath Fee и подпишитесь на бесплатную пробную версию.
Ознакомьтесь со структурой Cuemath Fee и подпишитесь на бесплатную пробную версию.
15 лучших математических трюков, которые сделают процесс обучения супер-пупер увлекательным для детей
Математика — предмет, с которым у многих детей возникают трудности. Нередко дети в конце концов теряют интерес к развитию своей числовой грамотности, из-за чего справляться с математикой становится все труднее по мере того, как они переходят в среднюю и старшую школу.
Крайне важно снабдить детей инструментами (или хитростями!), которые помогут им уверенно и легко решать математические задачи. Но о каких инструментах мы вообще говорим? Математические трюки могут быть полезны для детей несколькими способами. Они могут помочь им сократить количество шагов, необходимых для решения проблемы и достижения правильного решения.
Они также могут предложить детям различные подходы к решению одной и той же проблемы. Понимание математических трюков может в конечном итоге сделать математику более интересной и менее сложной для детей. Так почему бы не дать им вихрь? Вот несколько математических трюков с ответами и примерами, которые помогут вам быстро сообразить.
Так почему бы не дать им вихрь? Вот несколько математических трюков с ответами и примерами, которые помогут вам быстро сообразить.
Начнем!
Математические трюки для детей, которые стоит попробовать
1.
Умножение больших чисел в уме
Умение умножать большие числа является основным компонентом математики для детей как средней, так и старшей школы. Способность умножать большие числа в уме без какой-либо внешней помощи может помочь детям улучшить как свою скорость, так и способность решать вопросы, связанные с умножением.
Отличный способ умножить два двузначных числа — использовать их расстояние от 100, чтобы упростить математику. Давайте обсудим шаги. Мы найдем 95×97 с помощью этого трюка.
Шаг 1: Вычтите каждое число из 100.
100 − 95 = 5 и 100 − 97 = 3
Шаг 2: Сложите полученные значения (5 и 3) вместе.
Сумма = 5 + 3 = 8
Шаг 3: Вычтите эту сумму из 100, что даст нам первую часть ответа.
Первая часть ответа = 100 − 8 = 92
Шаг 4: Вторую часть ответа можно получить, перемножив 5 и 3! Вуаля!
Вторая часть ответа = 5 × 3 = 15
Таким образом, 95 × 97 = 9215
SplashLearn пробуждает любознательность на протяжении всей жизни своей игровой программой обучения PreK-5, которую любят более 40 миллионов детей. С более чем 4000 веселых игр и занятий, это идеальный баланс между обучением и игрой для вашего малыша.
Попробуйте бесплатно
2.
Сложение больших чисел
Когда дело доходит до математики, легко забыть, что сложение и вычитание могут быть такими же сложными для некоторых детей, как умножение и деление. Есть несколько трюков, которые они могут использовать, чтобы складывать числа в уме, весело и просто.
Один из самых простых способов заключается в использовании позиционных систем. Сложим 81 и 45, используя этот трюк.
Разбейте числа, используя разрядные значения (известные как расширенная форма чисел).
81 = 80 + 1
45 = 40 + 5
Сложите десятки и прибавьте к этой сумме цифры, стоящие на единице. Вот и все!
80 + 40 = 120
5 + 1 = 6
Итак, 81 + 45 = 120 + 6 = 126
3.
Умножение числа на 6
Никогда не знаешь, когда тебе понадобится умножить число на 6. К счастью, есть хитрость, позволяющая сделать это быстро и без особых усилий!
При умножении четного числа на 6 результирующее значение всегда будет заканчиваться той же цифрой, на которую вы умножили 6. Мы найдем только цифру десятков.
Рассмотрим 6 x 8. Произведение закончится на 8. Найдем разряд десятков.
Разделите значение, которое вы хотите умножить на 6, на 2. В этом случае мы разделим 8 на 2.
8 ÷ 2 = 4
Возьмите полученное значение, которое здесь равно 4, и поместите его перед числом, на которое вы умножаете 6. Другими словами, поместите 4 перед 8, и у вас будет 48!
4.
 Умножение числа на 9
Умножение числа на 9
Умножить любое число на 9 проще, чем вы могли себе представить! Возьмите любое большое значение. Давай 873! Поймите, как работает этот трюк.
873 × 9 = 873 × (10 − 1) = 8730 – 873 = 7857
Все, что вам нужно сделать, это умножить это большое число на 10, что даст вам 8730. Теперь вам просто нужно вычесть 873 из этого произведения. Полученное значение, 7857, является ответом, и это именно то, что вы получили бы, умножив 9.с 873!
Взгляните еще на два примера.
586 × 9 = 586 × (10 − 1) = 5860 − 586 = 5274
211 × 9 = 211 × (10 − 1) = 2110 − 211 = 1899 Способы Умножение чисел чуть больше 100 за 3 секунды
Ведические математические приемы Дети не поверят
1.
Сложение
Ведический математический прием для упрощения сложения заключается в том, чтобы сосредоточиться на ближайшем кратном 10 для каждого из чисел. участие, чтобы сделать процесс легким. Складываем 28 и 97 в качестве примера.
Складываем 28 и 97 в качестве примера.
Как бы вы сложили эти большие двузначные числа? Этот ведический трюк заставит вас найти и сложить их ближайшие кратные 10.
Шаг 1 : кратное 10, ближайшее к 28, равно 30. кратное 10, ближайшее к 97, равно 100.
Сложение их даст нам 100 + 30 = 130.
Шаг 2: Вычтите исходные числа из их ближайших кратных 10.
30 − 28 = 2 и 100 – 97 = 3
Сумма 2 и 3 равна 5. Просто вычтите 5 из 130. .
130 − 5 = 125, это и есть ваш ответ! Не может быть проще, чем это!
Дополнительная литература: Как упростить сложение и вычитание дробей например 1000, 10000 или 100000 легко получить с помощью этого трюка с ведической математикой! Это простой трюк, который включает в себя всего несколько умственных шагов. Здесь количество нулей должно совпадать с количеством цифр в вычитаемом числе.Возьмем в качестве примера 432! Вычтите все цифры, кроме цифры единиц, из 9 и вычтите цифру единиц из 10.
Если вам нужно вычесть 432 из 1000 (3 нуля и 3 цифры совпадают), вычтите первые две цифры 432 из 9 (9 - 4). = 5 и 9 - 3 = 6) и вычесть последнюю цифру 432 из 10 (10 - 2 = 8).
Это дает нам 5, 6 и 8, и ваш ответ 568!
Рассмотрим другой пример. Если количество цифр не совпадает, добавьте нули перед числом.
10 000 − 754 = 10 000 − 0754 = 9246
Попробуйте вычесть 568 из 10 000 и 8374 из 100 000, чтобы увидеть, насколько хорошо вы поняли этот простой трюк!
3.
Квадратные корниХотя сама по себе это и не трюк, ведическая математика предоставляет ряд полезных подсказок, которые помогут вам определить квадратный корень из числа. Прежде всего, мы должны понимать, что числа, оканчивающиеся на 2, 3, 7 и 8, не являются идеальными квадратами.
Это означает, что всякий раз, когда вы видите число, оканчивающееся на цифру 2, 3, 7 или 8, можно с уверенностью заключить, что это число не имеет полного квадратного корня (или целого числа в виде квадратного корня).
Если полный квадрат заканчивается на 1, например, 121 или 81, его квадратный корень всегда будет заканчиваться на 1 или 9.. Полный квадрат, оканчивающийся на 4, например 4 или 64, всегда будет иметь квадратный корень, оканчивающийся на 2 или 8!
4.
КвадратыВедический математический прием позволяет очень просто определить квадратное значение числа! Возьмем, к примеру, 98. Как бы вы нашли квадрат 98? Ваша база здесь будет 100.
Найдите отличие числа от базы. Другими словами, нам пришлось бы вычесть 100 из 98.
100 − 98 = 2.
Вычтите 2 из исходного числа, которое в данном примере равно 98.
98 − 2 = 96
Умножьте это число на основание.
96 x 100 = 9800.
Последнее, что вам нужно сделать, это прибавить квадратное значение 2, что равно 4, к 9800.
9800 + 4 = 9804 становится нашим ответом!
Математические трюки с числами для детей
1.
Математические трюки на день рожденияЕсли вы ищете забавный математический трюк на день рождения, который также может помочь вам улучшить вашу числовую грамотность, то у нас есть идея для ты! Для этого требуется несколько шагов, поэтому вы можете сесть и взять калькулятор.

Шаг 1: Добавьте 18 к числу месяца вашего дня рождения. Январь, например, в этом случае будет равен 1, а май будет равен 5.
Шаг 2: Умножьте полученное значение на 25, а затем вычтите 333!
Шаг 3: Умножьте новое значение на 8, а затем вычтите 554!
Шаг 4 : Разделите новое значение на 2 и добавьте дату своего рождения.
Шаг 5: Умножьте новое значение на 5 и прибавьте 692 на новое значение.
Шаг 6: Умножьте новое значение на 20 и добавьте две последние цифры года вашего рождения.
Шаг 7: Вычтите число 32940 из последнего значения и посмотрите на полученное число!
На ком бы вы ни пробовали этот трюк, ответ всегда даст нам дату рождения человека в формате ДД-ММ-ГГ! Не верьте нам на слово! Попробуйте сами!
2.
Трюк с 1089Вот еще один трюк, который вы можете попробовать на ком-то, который оставит его ошеломленным! Пока вы делаете это правильно, число, которое вы получите, всегда будет 1089.
!
Для начала попросите кого-нибудь записать любое трехзначное число. Попросите их переставить единицы трехзначных чисел, которые они написали, в порядке возрастания и убывания.
Если число, которое они записали, равно 603, то число в порядке убывания будет 036, а в порядке возрастания - 630. После этого попросите человека вычесть убывающее расположение из восходящего расположения.
Теперь у них должно быть число 594. Попросите их поменять это значение на обратное и прибавить к 59.4. Другими словами, 594 + 495 — это то, как должен выглядеть следующий шаг.
Какое бы трехзначное число ни выбрал человек, ответ всегда будет 1089! Попробуй сам!
3.
The 37 TrickЕсли вы хотите произвести впечатление на своих друзей и семью классной математической задачей, которая всегда приводит к значению 37, то вам повезло! Все, что вам нужно сделать, это выбрать любое трехзначное число с одинаковыми цифрами.
Возьмем, к примеру, 666.
Все, что вам нужно сделать, это сложить три цифры вместе. В этом случае 6 + 6 + 6 дает нам 18. После этого просто разделите 666 на 18. Есть предположения? Это верно! 37.
Это простой трюк, который работает с любым трехзначным числом с теми же тремя единицами! Получайте удовольствие, впечатляя своих друзей и семью этим трюком!
4.
Трюк 15В качестве последнего трюка мы обсудим еще один трюк, который дает одинаковое значение независимо от того, с какого числа вы начинаете! В этом ответ всегда будет 15.
Начните с того, что попросите друга выбрать число. Попросите их умножить это число на 3. После этого попросите их добавить 45 к полученному значению. Когда они это сделают, попросите их умножить ответ на 6, а затем разделить на 18.
На последнем шаге попросите их вычесть число, которое они выбрали в самом начале, из самого нового значения. Независимо от того, с какого числа они начали, ответ всегда будет 15!
В довершение всего, вы можете притвориться, что читаете мысли своего друга, и сказать ему, что ответ будет 15, как только он выполнит все эти шаги! Такие математические трюки обязательно произведут впечатление!
Похожие чтения: Лучшие математические приложения для учащихсяПростые математические трюки для детей
1.
Складывание двузначных чисел
Существует очень быстрый способ сложения двузначных чисел! Для этого фокуса возьмем 56 и 79.
Начнем с разделения второго числа на десятки и единицы. Это дает нам 70 и 9! Давайте проследим за этим, добавив 70 к 56, что даст нам 126. Все, что нам осталось сделать, это добавить 9 к 126, что даст нам ответ, 135!
Разбиение чисел на десятки и единицы может быть молниеносным подходом к сложению двузначных чисел и трюком, который стоит держать в рукаве!
2.
Умножение чисел на 15
Вы просто никогда не знаете, когда вам может понадобиться умножить число на 15! К счастью, есть простой трюк, который поможет вам в этом, и состоит всего из трех шагов. Возьмем для примера 69.
Сначала вам нужно добавить 0 в конце 69. Затем вам нужно разделить полученное значение 690 на 2, что даст вам 345.
Для вашего последнего шага все, что вам нужно сделать это добавить 690 к 345, что дает нам 1035! И вот оно!
Как это работает? Поймите, что умножение на 5 эквивалентно умножению на 10 и последующему делению на 2.
69 x 15 = 69 x (10 + 5) = 690 + (69 x 5) = 690 + 345
Математика не требует быть сложной темой, которая отпугивает студентов. С помощью нескольких приемов даже самые сложные проблемы можно решить мысленно! Освоение этих приемов может не только вселить уверенность в учеников, но и улучшить их числовую грамотность!
3.
Умножение двузначного числа на 11
Возможно, вам нечасто приходится умножать двузначное число на 11, но если вам это нужно, этот трюк поможет вам сэкономить время! Возьмем, к примеру, 32. Как бы вы быстро умножили 32 на 11?
Вы должны начать с вычисления суммы 3 и 2, что дает нам 5. Достаточно просто? Затем вам нужно поместить сумму этих цифр, 5, между 3 и 2. Это даст нам 352. Давайте попробуем еще раз с другим числом. На этот раз возьмем 51.
Что получится, если сложить 5 и 1? 6! Все, что нам нужно сделать с этого момента, это поставить 6 между 5 и 1, чтобы получить 561!
Однако об этом трюке нужно помнить одну вещь.
Что делать, если аддитивное значение цифр представляет собой двузначное число? Рассмотрим 67 x 11.
6 + 7 = 13
Поместите это число между цифрами и прибавьте к 13 разряд десятков, что равно 1. Таким образом, мы получим от 1 до 6;
6(13)7 = (6+1)(3)7 = 737Немного практики с этими трюками может помочь сделать математику более увлекательной, полезной и менее сложной для учащихся, желающих приложить усилия, чтобы освоить их!
Часто задаваемые вопросы (FAQ)
Какие математические трюки дети должны осваивать в первую очередь?
Некоторые трюки сложнее понять, чем другие. Однако то, будет ли ученику труднее умножать числа на 11 в уме или вычислять квадраты меньших чисел, полностью зависит от них!
Какому порядку или иерархии я должен следовать, чтобы учить своих детей математическим формулам и трюкам в уме?
Нет необходимости следовать какому-то определенному порядку, и лучше позволить ребенку пройти через все это самостоятельно.
 Затем пронумеруйте каждый из ваших 10 пальцев, начиная с 1 до 10 и двигаясь от большого пальца левой руки к большому пальцу правой.
Затем пронумеруйте каждый из ваших 10 пальцев, начиная с 1 до 10 и двигаясь от большого пальца левой руки к большому пальцу правой.
 Таким образом, возьмите среднее число 9 и вычтите 5, это 9-5 = 4. Наконец, возьмите 9 в правом конце, вычтите 4 и найдите 9-4 = 5.
Таким образом, возьмите среднее число 9 и вычтите 5, это 9-5 = 4. Наконец, возьмите 9 в правом конце, вычтите 4 и найдите 9-4 = 5. Если вам нужно вычесть 432 из 1000 (3 нуля и 3 цифры совпадают), вычтите первые две цифры 432 из 9 (9 - 4). = 5 и 9 - 3 = 6) и вычесть последнюю цифру 432 из 10 (10 - 2 = 8).
Если вам нужно вычесть 432 из 1000 (3 нуля и 3 цифры совпадают), вычтите первые две цифры 432 из 9 (9 - 4). = 5 и 9 - 3 = 6) и вычесть последнюю цифру 432 из 10 (10 - 2 = 8).  Если полный квадрат заканчивается на 1, например, 121 или 81, его квадратный корень всегда будет заканчиваться на 1 или 9.. Полный квадрат, оканчивающийся на 4, например 4 или 64, всегда будет иметь квадратный корень, оканчивающийся на 2 или 8!
Если полный квадрат заканчивается на 1, например, 121 или 81, его квадратный корень всегда будет заканчиваться на 1 или 9.. Полный квадрат, оканчивающийся на 4, например 4 или 64, всегда будет иметь квадратный корень, оканчивающийся на 2 или 8! 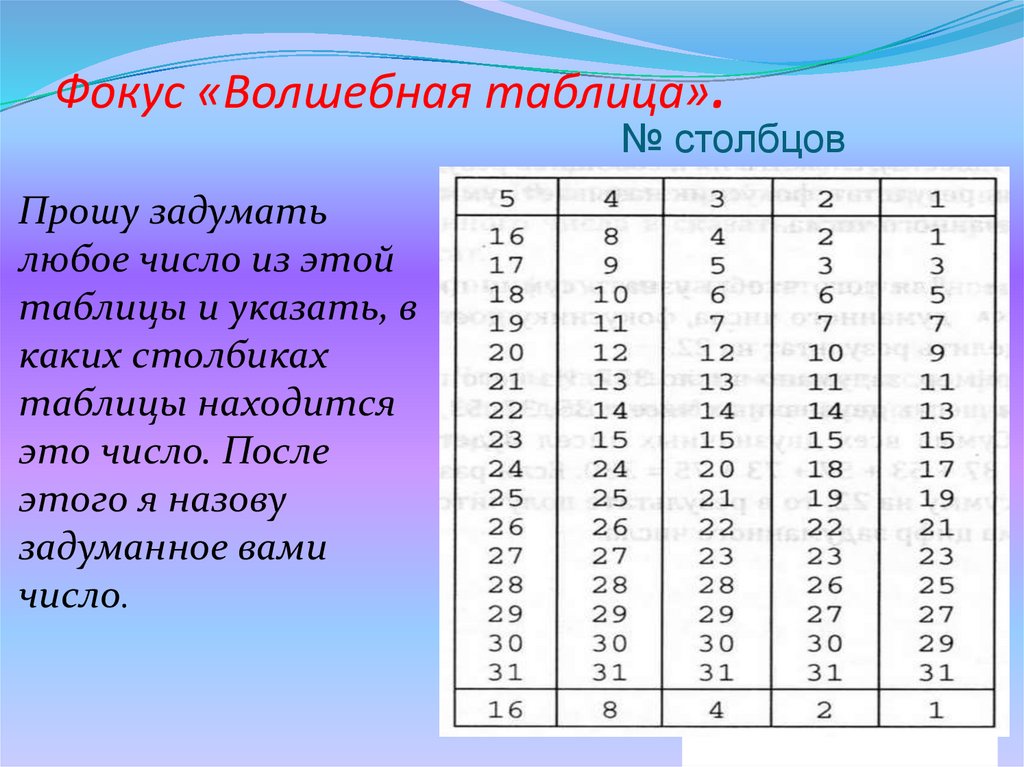
 !
!  Складывание двузначных чисел
Складывание двузначных чисел 
 Что делать, если аддитивное значение цифр представляет собой двузначное число? Рассмотрим 67 x 11.
Что делать, если аддитивное значение цифр представляет собой двузначное число? Рассмотрим 67 x 11.