Урок математики в 6-м классе по теме: «Умножение отрицательных чисел»
Цель: Научить умножать
положительные и отрицательные числа, а также
перемножать отрицательные числа.
Ход урока:
1. Устно:
Примеры записаны на карточках, классу
показываю карточки с примерами:
| 4/9 * 1/2 | 0 * 5/6 | 3/7 * 14 | 3 * 1/5 |
| 7/2 * 2/7 | 1/2 * 3/8 | 7 * 4/9 * 1/7 | 5,6 * 1/7 |
| 3/2 * 2/3 | |||
2. Историческая справка:
Индийский математик Брамагупта, живший в VII
веке, пользовался отрицательными числами.
Положительные числа представлял как
“имущества”, Отрицательные числа как “долги”.
Правила сложения положительных и отрицательных
чисел он выражал так:
ПЛАКАТ
| “Сумма двух имуществ — имущество (+
Сумма двух долгов есть долг
(-X)+ (-X)= (-X)”. |
Условившись положительные числа связывать со
словом “друг”, а отрицательные числа со словом
“враг”, древние употребляли интересное правило
умножения:
ПЛАКАТ
| “Друг моего друга — мой друг (+X) * (+X)= (+X)
Друг моего врага — мой враг
(+X) * (-X)= (-X)
Враг моего друга — мой враг
(- X ) * (+ X )= (- X )
Враг моего врага — мой друг
(- X ) * (- X )= (+ X ) |
3. На доске записаны примеры:
(-12) * (-3)=
(-14) * (+5)=
(-14) * (-0,2)=
(-4,2) * 10=
(-6/7) * (-1/2)=
4/21
* (-7/16)=
(-2,4) * (-3)=6
-1,8 * 4=
Ребятам предлагается, используя правила
умножения древних людей вычислить данные
примеры.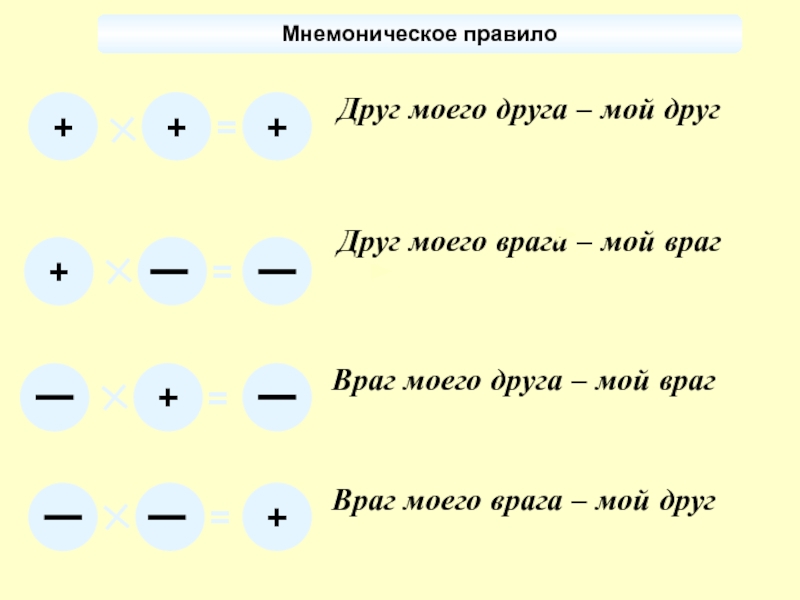
Когда примеры решены, прошу учеников попробовать
сформулировать правило умножения двух
отрицательных чисел и правило умножения двух
чисел с разными знаками.
Затем открываем учебник, читаем правила,
сравниваем их с теми, которые мы вывели сами,
делаем вывод, как умножить два отрицательных
числа, как умножить два числа с разными знаками:
1. Надо
указать какое действие.
2. Какие
знаки имеют множители.
3.
Установить знак результата.
4. Найти
модуль произведения.
Рассмотрим № 1105 (а — м) по цепочке с места, с
комментарием.
4. На доске записаны примеры:
а) (-7) * (-5) * 2=
(-4) * (-10) * 8=
б) (-2) * (-3) * (-4)=
(-1,2) * (-2) * (-12)=
в) (-1) * (-2) * (-5) * (-15) * 2=
Надо определить знак произведения и вычислить.
После этого спрашиваю, какой вывод можно сделать
относительно знака произведения, где чётное
(нечётное) число отрицательных множителей?
Если число отрицательных множителей нечетное, то
произведение — число отрицательное.
Если число отрицательных множителей чётное, то
произведение — число положительное.
5.а) Работа с учебником.
№ 1105 (н- т) — двое у
доски
№ 1107 (три ученика у
доски) по одной строчке
5.б) Вычислить: (примеры записаны на доске)
| а) –2,4 * 2 * (-0,5)= | г) 0,2 * (-100) * 3 * 1/3= |
| б) –1/2 * 4/9 * (-27/28) * (-56/57)= | д) 2 * (-3) * 4 * (-5) * 6= |
| в) –9 * 2 * (-3) * 1/2= | е) –2,3 * (-2) * (-8)= |
6. Самостоятельная работа через копировку:
| Вариант 16 | Вариант 2 | ||
| 1) –64 * 10= | (-640) | 1) (-5,8) * 10= | (-58) |
| 2) (-2,8) * 3= | (-8,4) | 2) 82 * (-3)= | (-246) |
| 3) (-4,7) * (-5)= | (23,5) | 3) (-5,4) * (-7)= | (37,8) |
| 4) 6,9 * (-0,1)= | (-0,69) | 4) 1,9 * (-0,1)= | (-0,19) |
| 5) (-6,08) * (-100)= | (608) | 5) (-8,6) * (-100)= | (860) |
| 6) 4/7 * (-7/8)= | (-1/2) | 6) (-3/7) * 7/9= | (-1/3) |
| 7) -4,4 * 5/11= | (-2) | 7) –14/5 * 5/28= | (-1/2) |
| 8) –6,02 * (-3,8)= | (22,876) | 8) –8,06 * (-2,3)= | (18,538) |
| 9) –11/8 * 40/33= | (-5/3) | 9) –13/4 * 40/39= | (-10/3) |
| 10) –8/3 * 9/4= | (-6) | 10) –7/2 * 30/7= | (-15) |
Тетрадь сдаем, “копирку” проверяем, на доске
приведена таблица оценок.
8 — 10 примеров решены верно — оценка “5”
7-6 примеров
— оценка “4”
5-4 примеров
— оценка “3”
Ещё раз повторяем, как умножать два
отрицательных числа, как умножать два числа с
разными знаками.
7. Итоги урока, оценки
Домашнее задание: № 1127, № 1128.
3. Враг моего врага . Удовольствие от X. Увлекательное путешествие в мир математики от одного из лучших преподавателей в мире
В начальной школе вычитание учат сразу после сложения. И в этом, безусловно, есть смысл: в обоих случаях применяется счет чисел, только при вычитании он выполняется в обратную сторону. Психологически действия тоже похожи: ребенок учится брать и давать примерно в одно и то же время. Сложение и вычитание всегда идут рука об руку. Если человек готов посчитать, сколько будет 23 + 9, то не сомневайтесь, он скоро ответит и на вопрос, сколько будет 23 – 9.
Но если углубиться в эту тему, то в отличие от сложения вычитание создает довольно неприятную проблему, поскольку в результате могут появиться отрицательные числа. Если я захочу взять у вас 6 булочек, а у вас их только 2, то в реальности у меня ничего не получится. Зато в уме я навешу на вас 4 отрицательные булочки, что бы это ни значило.
Если я захочу взять у вас 6 булочек, а у вас их только 2, то в реальности у меня ничего не получится. Зато в уме я навешу на вас 4 отрицательные булочки, что бы это ни значило.
Вычитание заставляет нас расширить свое представление о числах. Отрицательные числа более абстрактны, чем положительные. Четыре отрицательные булочки не потрогаешь и не съешь, зато их можно представить. Самое интересное, что в реальном мире отрицательные числа тоже встречаются: долги, перерасход по кредитной карте, минусовые температуры зимой и обозначения подвальных уровней на крытых парковках.
Многие из нас пока еще не заключили мир с отрицательными числами. Как заметил мой коллега Энди, люди придумали всевозможные забавные мелкие уловки, чтобы обойти страшный отрицательный знак «минус». В отчетах паевых инвестиционных фондов потери (отрицательные числа) печатаются красным или заключаются в круглые скобки, чтобы минусы ни в коем случае не появились. В исторических книгах сказано, что Юлий Цезарь родился в 100 году до н. э., а не в –100 году. Подземные уровни парковки часто обозначаются как B1 и B2. Температура – одно из немногих исключений, когда люди действительно говорят, что она составляет –5 градусов, хотя и в этом случае многие предпочитают фразу «5 градусов ниже нуля». Видимо, в отрицательном знаке есть нечто отталкивающее и… негативное.
э., а не в –100 году. Подземные уровни парковки часто обозначаются как B1 и B2. Температура – одно из немногих исключений, когда люди действительно говорят, что она составляет –5 градусов, хотя и в этом случае многие предпочитают фразу «5 градусов ниже нуля». Видимо, в отрицательном знаке есть нечто отталкивающее и… негативное.
Возможно, самое неприятное заключается в том, что при перемножении двух отрицательных чисел получается положительное число. Поэтому позвольте привести доводы в защиту знака минус.
Как нам определить ценность такого выражения, как –1 ? 3, где мы умножаем отрицательное число на положительное? Ну хорошо, так как 1 ? 3 означает сумму 1 + 1 + 1, естественно представить –1 ? 3 как (–1) + (–1) + (–1), что равняется –3. Это должно стать очевидным в примере с деньгами: если вы должны мне 1 доллар в неделю, то по истечении трех недель вы мне будете должны 3 доллара.
Отсюда уже недалеко до понимания, почему минус, умноженный на минус, дает плюс. А теперь взгляните на следующий ряд равенств:
– 1 ? 3 = –3
– 1 ? 2 = –2
– 1 ? 1 = –1
– 1 ? 0 = 0
– 1 ? –1 =?
Посмотрите на числа в правой части равенств и удостоверьтесь в том, что это обычная прогрессия: –3, –2, –1, 0… На каждом шаге мы добавляем 1 к предыдущему числу. Таким образом, разве не логично, что следующим числом будет 1?
Таким образом, разве не логично, что следующим числом будет 1?
Это один аргумент в пользу того, почему (–1) ? (–1) = 1. Привлекательность такого толкования заключается в том, что оно позволяет сохранить правила обычной арифметики – получается, что они верны как для положительных, так и для отрицательных чисел.
Но если вы бесчувственный прагматик, то, вероятно, будете удивлены, что у этих абстракций есть некие параллели в реальном мире. По общему признанию, жизнь иногда играет по различным правилам. В обычных этических построениях два заблуждения не приводят к истине. Более того, двойные отрицания не всегда равнозначны утверждению; они могут усилить отрицание, как в случае с «Я не могу получить никакого удовлетворения». (Действительно, в этом отношении язык может быть очень мудреным. Выдающийся британский философ и лингвист Дж. Остин из Оксфорда как-то в своей лекции заявил, что во многих языках двойное отрицание дает утверждение, но ни в одном дважды повторенное утверждение не дает отрицания. На что сидевший в аудитории философ из Колумбии Сидни Мордженбессер ехидно процедил: «Да-да».)
На что сидевший в аудитории философ из Колумбии Сидни Мордженбессер ехидно процедил: «Да-да».)
Тем не менее есть немало случаев, когда реальный мир действительно отражает правила умножения отрицательных чисел. Например, возбуждение одной нервной клетки может быть подавлено возбуждением второй нервной клетки. Если в этот момент возбуждение второй нервной клетки подавляется третьей нервной клеткой, то первая клетка может снова возбудиться. Косвенное воздействие третьей клетки на первую вызывает ее возбуждение. Таким образом, последовательность двух отрицаний приводит к утверждению. Подобные эффекты происходят и при регуляции генов: белок может включить ген, блокируя другую молекулу, которая подавляла этот отрезок молекулы ДНК.
Возможно, самую понятную параллель можно провести в социально-политической сфере. Как утверждает пословица, «враг моего врага – мой друг». Общеизвестно, что понятия вроде «друг моего врага», «враг моего друга» и тому подобные можно подставить в виде треугольника отношений. {6}
{6}
В углы треугольника помещают людей, компании или страны, а соединяющие их стороны показывают отношения между ними, которые могут быть как позитивными, или дружественными (обычно отображаются сплошными линиями), так и негативными, или враждебными (отображаются пунктирными линиями).
Социологи строят треугольники, подобные треугольнику слева, то есть считая отношения между объектами позитивными, так как разумно любить друзей ваших друзей. Точно так же треугольник справа, с двумя негативными и одной позитивной связью, считается сбалансированным, потому что такая комбинация не вызывает разногласий, даже несмотря на две стороны с негативными связями, поскольку ничто так не цементирует дружбу, как ненависть к одному и тому же человеку.
Конечно, треугольники могут быть выведены из состояния баланса. Это происходит в ситуации, когда есть три врага, причем двое из них относятся друг к другу менее враждебно и готовы объединиться, чтобы напасть на третьего.
Еще менее сбалансированным будет треугольник с единственной негативной связью. Например, предположим, что Кэрол хорошо относится и к Элис, и к Бобу, но Боб и Элис не любят друг друга. Возможно, они когда-то встречались и пережили тяжелое расставание, и теперь говорят друг о друге гадости лояльной к обоим Кэрол. Это создает психологическое напряжение между всеми тремя. Чтобы восстановить баланс, либо Элис и Боб должны урегулировать свои отношения, либо Кэрол должна принять чью-то сторону.
Например, предположим, что Кэрол хорошо относится и к Элис, и к Бобу, но Боб и Элис не любят друг друга. Возможно, они когда-то встречались и пережили тяжелое расставание, и теперь говорят друг о друге гадости лояльной к обоим Кэрол. Это создает психологическое напряжение между всеми тремя. Чтобы восстановить баланс, либо Элис и Боб должны урегулировать свои отношения, либо Кэрол должна принять чью-то сторону.
Во всех этих случаях логика баланса соответствует логике умножения. В сбалансированном треугольнике знак произведения двух любых сторон, положительный или отрицательный, всегда совпадает со знаком третьей стороны. В несбалансированном треугольнике это правило нарушается.
Не будем касаться вопросов о правдоподобии приведенных моделей, ибо здесь возникают интересные вопросы с чисто математическим привкусом. Например, в связной сети, где все друг друга знают, какое самое устойчивое состояние? Прежде всего это нирвана доброжелательности, где все отношения позитивные, а все треугольники в пределах сети сбалансированы. Однако существуют и другие устойчивые состояния. Например, устойчивое к конфликтам состояние, когда сеть раскололась на два враждебных лагеря (произвольных по величине и составу). Все члены одного лагеря хорошо относятся друг к другу, но враждебны к представителям другого лагеря. (Ничего не напоминает?) Возможно, еще более удивительно то, что эти полярные состояния являются единственно возможными столь же устойчивыми состояниями, как нирвана{7}. В частности, ни у какого трехстороннего раскола не может быть уравновешенных треугольников.
Однако существуют и другие устойчивые состояния. Например, устойчивое к конфликтам состояние, когда сеть раскололась на два враждебных лагеря (произвольных по величине и составу). Все члены одного лагеря хорошо относятся друг к другу, но враждебны к представителям другого лагеря. (Ничего не напоминает?) Возможно, еще более удивительно то, что эти полярные состояния являются единственно возможными столь же устойчивыми состояниями, как нирвана{7}. В частности, ни у какого трехстороннего раскола не может быть уравновешенных треугольников.
Ученые использовали этот метод для анализа союзов, сложившихся при подготовке к Первой мировой войне{8}. Диаграммы, представленные ниже, показывают союзы между основными державами, участвовавшими в ней: Великобританией, Францией, Россией, Италией, Германией и Австро-Венгрией между 1872 и 1907 гг.
Первые пять конфигураций были несбалансированными, потому что каждая из них содержала по крайней мере один несбалансированный треугольник. Возникающие в результате разногласия подталкивали эти страны к изменению конфигурации, тем самым вызывая реверберацию в других частях сети. На последнем этапе Европа раскололась на два непримиримых антагонистских блока, придя к общему балансу, но оказавшись на грани войны.
Возникающие в результате разногласия подталкивали эти страны к изменению конфигурации, тем самым вызывая реверберацию в других частях сети. На последнем этапе Европа раскололась на два непримиримых антагонистских блока, придя к общему балансу, но оказавшись на грани войны.
Однако это не значит, что на основании данной теории можно делать прогнозы. Это не так. Подобный подход не позволяет объяснить все тонкости изменений в геополитике. Но некоторые из наблюдаемых нами явлений происходят в соответствии именно с примитивной логикой «враг моего врага» и отлично подпадают под умножение отрицательных чисел. Отделяя важное от незначительного, арифметика отрицательных чисел может помочь нам отыскать настоящие загадки.
Данный текст является ознакомительным фрагментом.
Математика дружбы
Помните соседских детей, с которыми вы росли? С теми, с кем ты будешь играть с того момента, как выйдешь из школы, и до тех пор, пока все не отправятся домой на ужин?
Эти друзья определяют нашу жизнь, они заставляют нас улыбаться даже после того, как прошло детство. Но если быть честными, это были отношения, которые не требовали особых усилий.
Но если быть честными, это были отношения, которые не требовали особых усилий.
Подобно дружбе между взрослыми, некоторые из этих отношений основывались на удобстве. Вот простая математика: возьмите одного человека и поместите рядом с ним второго человека, оба из которых заинтересованы во взаимодействии, а затем сложите их вместе. Что вы получаете? Мгновенный друг!
Я не хочу преуменьшать важность дружеских отношений по расчету — где бы они ни начинались — в офисе, спортзале или книжном клубе. Я также не хочу умалять ту роль, которую эти основные друзья играли и продолжают играть в моей жизни. Некоторые из этих отношений отражают комфорт и стойкость C.C. и дружба Хиллари в Beaches .
Большинство друзей не такие, правда? Во взрослом возрасте дружба больше похожа не на простое сложение, а на алгебраическую задачу с переменными. Вопрос о том, может ли уникальный набор (X) личных предпочтений, (Y) образа жизни и (Z) этики двух людей быть одинаковым с обеих сторон.
С одной стороны, проницательность — это хорошо. Когда я стал старше, меня гораздо меньше заботит количество людей, которым я нравлюсь. Будучи интровертом, я больше ценю качество, чем количество. Я хочу общаться с людьми, которые приносят энергию в мою жизнь. Я научилась наслаждаться дружбой с собой, местом, где я перезаряжаюсь и нахожу покой. Итак, дружба — это более интимное предложение, которое я не распространяю на каждого знакомого.
С другой стороны, то, что кажется защищающим, может быть одиноким. Такая избирательность в отношении того, кого я впускаю в свою личную жизнь, резко снижает количество моих друзей. Мне легче быть одному, чем большинству, но я также признаю важность общения.
Тем не менее, я не хочу идти на компромисс со своими стандартами дружбы.
Алгебра ожиданий
Мы все ожидаем от друзей одного и того же: взаимной радости. Наши отношения должны питать наши души и развивать наш потенциал, но достижение этого не является ни конгруэнтным, ни симметричным.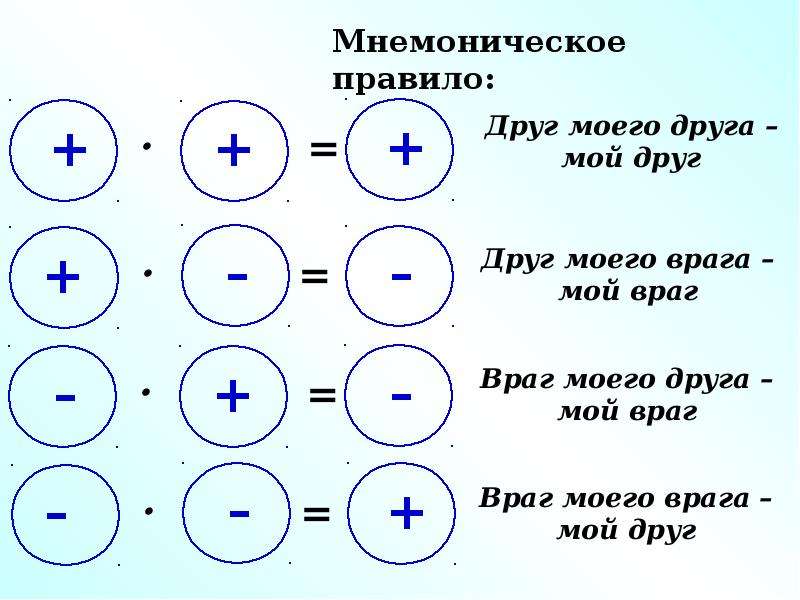
Внутри каждой дружбы есть невидимая шкала. Иногда вы добавляете к шкале больше, чем другой человек, и наоборот. Этот толчок и притяжение могут быть полностью равными или последовательно односторонними. На самом деле баланс не имеет значения, пока обе стороны чувствуют себя удовлетворенными.
Результат на шкале во многом зависит от типа вашей дружбы. Дружба с людьми, с которыми вам нравится гулять, и ничего более, вероятно, имеет очень мало значения на шкале, но обе стороны могут быть относительно равными.
В других случаях распределение на весах определяется потребностями каждой стороны. Например, если близкий друг потерял родителей, вы будете давать больше в течение определенного периода времени, и это нормально.
Я счастлив быть рядом с другом, переживающим трудности. Я люблю помогать, даже если они не могут предложить мне то же самое взамен. Я не чувствую себя опустошенным в этих дружеских отношениях, потому что я счастлив отдавать.
Фракции дружбы
Иранцы — мастера гостеприимства. Мы подписываемся на мантру: «Ваш комфорт — мой комфорт». Я всегда хочу, чтобы у других все было хорошо, что часто проявляется в моей дружбе. В этот момент мне приходится напоминать себе, что у меня тоже есть потребности.
Мы подписываемся на мантру: «Ваш комфорт — мой комфорт». Я всегда хочу, чтобы у других все было хорошо, что часто проявляется в моей дружбе. В этот момент мне приходится напоминать себе, что у меня тоже есть потребности.
Многие из нас не умеют угождать. Мы откладываем свои потребности на второй план, чтобы позаботиться о ком-то другом, будь то партнер, член семьи, друг или даже незнакомец. К сожалению, это создает нереалистичные ожидания и совершенно неустойчиво.
Неудивительно, что любители часто пытаются сбалансировать свою дружбу. Несмотря на то, что перенос большего веса на весы иногда приемлем, брать на себя большую часть веса при каждом взаимодействии нельзя.
Угодники мотивированы двумя вещами: желанием избежать конфликта и желанием нравиться. Я понимаю — мы все хотим нравиться людям. Мотивация большинства угодников служить другим именно такова, но стоит ли это того?
Когда вы угождаете другим за счет служения себе, вы теряете свою силу. Хотя власть не является фактором, обычно связанным с друзьями, она является важной переменной в любых отношениях.
Когда у тебя нет силы, ты несешь всю тяжесть дружбы. Чаша весов склоняется в пользу другого человека, открывая дверь в токсичные отношения. Где в этом удовлетворение?
Хронически несбалансированная дружба не приносит взаимного удовольствия. Ваши отношения должны приносить вам радость, а не умалять ваше счастье.
Абсолютная ценность дружбы
Когда я размышляю о дружбе и о том, что она на самом деле значит для меня, я не могу не думать о тех друзьях из прошлого. Я до сих пор общаюсь с некоторыми из них, и когда мы собираемся вместе, это волшебство.
Вместо того, чтобы обмениваться любезностями и скользить по поверхности, мы ныряем туда, где остановились, независимо от того, как долго мы были в разлуке. Независимо от того, началась ли наша связь в старшей школе, колледже или в первые годы нашей профессиональной карьеры, она остается неизменной. Несмотря на то, что жизнь и география помешали, здесь все же есть что-то особенное. Мы проводим вместе несколько часов, и кажется, что мы никогда не прощались.
Эти эмоциональные, духовные привязанности неподвластны времени. Годы прошли друг без друга, но любовь и близость остались. Жестокая ирония в том, что наши моменты вместе заставляют меня задуматься, почему я не уделяю больше времени таким моментам, как этот.
У двух главных героев фильма Beaches одинаковая интонация. Их жизнь ведет их в разные стороны, но они всегда находят дорогу друг к другу. Даже если их встречи не всегда приятны, наблюдение за их общением является важным напоминанием о той судьбоносной роли, которую дружба играет в нашей жизни, если мы позволим ей это сделать.
Дружба должна приносить ни с чем не сравнимую, пламенную радость. Лучшие союзы животворны, обильны и абсолютны. Они случаются не каждый день, но когда они случаются, их стоит развивать. Как бы не сложилась математика.
Подпишитесь на мою рассылку, чтобы первыми узнавать о моих предстоящих мероприятиях и получать советы о том, как можно более эффективно общаться и вести переговоры.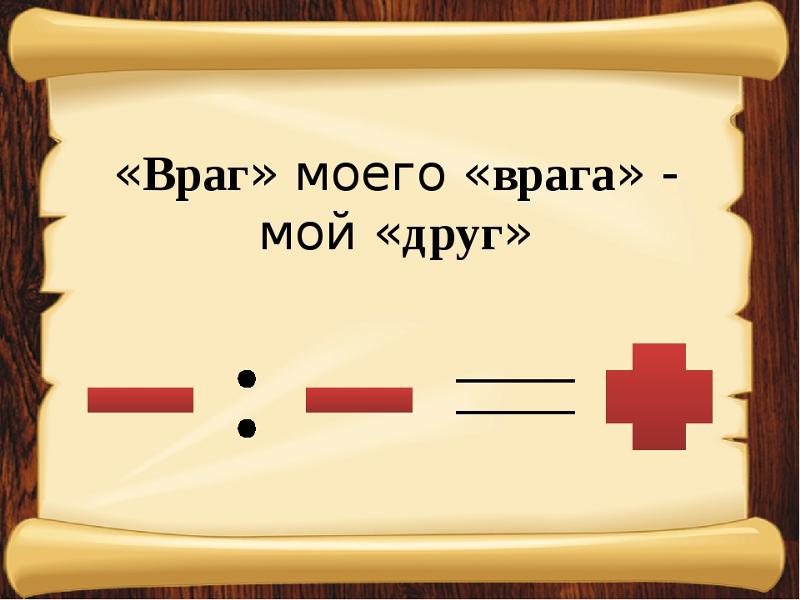
We’re Knot Friends – Math ∩ Programming
Снова апрельские холода.
В течение нескольких лет в старших классах и бакалавриате я работал вожатым в дневном лагере. Я уже писала о том, как это помогло мне развить навыки рассказывания историй, но недавно я снова вспомнила об этом, потому что, убирая шкаф, полный старого хлама, я наткнулась на пакет с нитками для вышивания. В то время как стереотипно используется для вшивания цветов в наволочку или надписи «дом, милый дом» на обруче, в летних лагерях нитью для вышивания делают браслеты дружбы.
Изображение от SarahMaker
Для тех, кто не знает, браслет дружбы представляет собой простую форму макраме, то есть дизайн создается путем завязывания узлов, а не плетения или плетения. Выкройки браслетов, как правило, достаточно просты для ребенка 8 или 9 лет, хотя и с небольшой практикой. Считается, что они возникли у коренных народов Америки, где узлы завязывались на веревке для отслеживания времени и счета, но в Соединенных Штатах их популярность среди детей возросла как символ дружбы в качестве подарка. Как гласит легенда, когда кто-то дарит вам браслет дружбы, вы надеваете его и загадываете желание, и вы должны оставить его до тех пор, пока браслет не спадет естественным образом, после чего ваше желание сбудется.
Как гласит легенда, когда кто-то дарит вам браслет дружбы, вы надеваете его и загадываете желание, и вы должны оставить его до тех пор, пока браслет не спадет естественным образом, после чего ваше желание сбудется.
Дети очень серьезно относятся к правилу «естественного падения» , но, оглядываясь назад, я нахожу другой аспект более увлекательным. Завязывание браслетов дружбы — это совместное занятие. Это повторяющаяся задача, которую вы не можете выполнять рассеянно, она занимает по крайней мере несколько часов, и вам нужно оставаться на месте, пока вы ее выполняете. Но вы можете наслаждаться общей компанией, и в конце концов вы сделали что-то красивое. Дети сидели в кругу, каждый работал над своим собственным браслетом, иногда даже прикрепляя их к рюкзакам друг друга по кругу, болтая о том, что занимало их мысли. Дети, которые, как правило, были гиперактивными и их было трудно загнать в угол, чудесным образом организовали себя в безмятежный, ритмичный фокус. И с ними было приятно сидеть и вязать, когда работа меня почему-то не оттягивала.
Думая об этом, я понимаю, как мало с тех пор я участвовал в общественной деятельности. Это похоже на то, как семья сидит вместе и готовит рождественское печенье, или группа художников рисует вместе. Люди жалуются, что в тридцать с небольшим трудно завести друзей, и мне интересно, насколько это просто потому, что мы не можем позволить себе время на такие совместные занятия. Мы не регулярно бываем среди групп людей, у которых есть свободное время, которое ускоряет эти моменты праздной связи.
Даже не думая об этом в то время, я, тем не менее, сделал изготовление браслетов дружбы своей специальностью. Я провел много времени, обучая детей, как их завязать. Не знаю, как я вжился в эту роль. Я подозреваю, что ремесленный аспект этого щекотал мой мозг, но в то время я и близко не осознавал свою любовь к мастерству, как сейчас. Я выучил дюжину или около того узоров и придумал способ связать двухцветный узор из букв, с помощью которого я мог писать имена людей пиксельным шрифтом. Это произвело впечатление на многих подростков.
Это произвело впечатление на многих подростков.
Десять лет спустя этот мешок с веревками смог проехать со мной через всю Америку через аспирантуру и множество квартир, и я подумал, что, может быть, смогу найти занятие по математике, связанное с узлами, узорами и… ну, что-нибудь математическое. Моя попытка превратить это в деятельность потерпела неудачу, но не по той причине, по которой я думал, что это могло бы быть. Оказывается, восьмилетние дети еще не обладают достаточной ловкостью, чтобы точно или эффективно завязывать браслеты, чтобы начать задавать вопросы о возможных узорах узлов. Я явно все еще акклиматизировался к диапазону способностей, типичному для того возраста.
После этого я подумал, почему бы не попробовать сделать еще раз? За прошедшие годы я время от времени видел паттерн, который явно не был построен с использованием известных мне техник. Чтобы уточнить, мне нужно кратко объяснить, как сделать простой браслет. По сравнению с другими формами художественного волокна, это довольно просто и не требует ничего, кроме ткацкого станка или вязальных спиц. Только веревка и что-то, чтобы держать кусок на месте.
Только веревка и что-то, чтобы держать кусок на месте.
Вы начинаете с того, что связываете все свои нити вместе в один узел на одном конце, прикрепляете его скотчем или прикрепляете булавками для натяжения и расправляете свои нити. Затем, используя крайнюю левую нить и постепенно перемещая ее слева направо, вы приступайте к завязыванию «стежков», где один «стежок» состоит из двух узлов левой нити поверх правой нити. В результате одного стежка «ведущая» строка (в данном случае самая левая) дает цвет, который отображается сверху, и «перемещается» вправо на одну позицию. Выполнение этого с одной и той же нитью на всех нитях приводит к (слегка диагональной) линии стежков одного цвета. После того, как вы закончите одну строку, теперь бывшая ведущая строка окажется на самом правом конце, и вы используете крайнюю левую строку в качестве новой ведущей строки.
Схема, показывающая, как связать одну петлю двумя нитками. Принимая во внимание «красный» стежок в качестве ведущей строки, этот «прямой стежок» оставляет начальный цвет сверху и перемещает ведущую нить на одну позицию вправо. В шагах 3 и 5 один и тот же узел завязывается дважды, но положение нити из шага 4 показывает цвет в последнем стежке. Узор «полоса», показывающий последовательность прямых стежков. Источник изображения
В шагах 3 и 5 один и тот же узел завязывается дважды, но положение нити из шага 4 показывает цвет в последнем стежке. Узор «полоса», показывающий последовательность прямых стежков. Источник изображения
Узор в виде полос обычно является одним из первых узоров, которые вы изучаете, потому что он очень прост. Но вы можете себе это представить, связывая нити в разном порядке и разумно выбирая, какая нить является «ведущей» нитью (то есть, какой цвет нити отображается в каждом стежке), вы можете создавать разнообразные узоры. Некоторые из них изображены в начале статьи. Тем не менее, смешанные узоры, которые я видел, не могли быть созданы таким образом, отчасти потому, что, во-первых, они были намного сложнее, чем можно построить в вышеописанном стиле (там явно есть какая-то ограничивающая структура). И, во-вторых, они использовали больше цветов, чем ширина браслета, а это означает, что новые цветные нити каким-то образом менялись местами в дизайне. Посмотрите, например, на эти коровьи браслеты.
Эту милую корову нельзя было сшить простой выкройкой. Источник изображения
В противном случае, не имея опыта работы с волокном, я не знал, и мне было любопытно, как это можно сделать. После недолгих поисков я нашел так называемые браслеты alpha , которые вскрыли корпус настежь.
Вместо того, чтобы использовать веревки в качестве конструкции для удержания узлов и вещей, которые завязывают узлы, альфа-браслет имеет веревки, которые проходят по всей длине браслета и служат только для того, чтобы завязывать на них узлы. По аналогии с ткачеством (о котором я еще несколько месяцев назад ничего не знала) различают нити основы и утка, а «классические» браслеты — нет. И поскольку мы завязываем узлы, цвет «основных» нитей никогда не отображается, кроме как на концах, когда они завязываются.
Чтобы получить больше цветов, существует немного сложный процесс «привязывания» новой нити, при котором старая ведущая нить продевается между двумя узлами, расположенными сверху, нового стежка и проходит под всей композицией. У Маши Узелков, ютубера браслетов, есть, пожалуй, самый популярный в Интернете учебник о том, как делать альфа-браслеты. Но благодаря этому поиску я также обнаружил веб-сайт браслетаbook.com, на котором есть сборник различных паттернов. Схемы на этом сайте прояснили для меня одно очевидное различие между «классическими» и альфа-браслетами: стежки классических браслетов лежат на срезанной решетке, а альфа-браслеты — на стандартной евклидовой сетке. И вы можете легко создать нотацию, описывающую, как связать узор.
У Маши Узелков, ютубера браслетов, есть, пожалуй, самый популярный в Интернете учебник о том, как делать альфа-браслеты. Но благодаря этому поиску я также обнаружил веб-сайт браслетаbook.com, на котором есть сборник различных паттернов. Схемы на этом сайте прояснили для меня одно очевидное различие между «классическими» и альфа-браслетами: стежки классических браслетов лежат на срезанной решетке, а альфа-браслеты — на стандартной евклидовой сетке. И вы можете легко создать нотацию, описывающую, как связать узор.
Классическая схема браслета из браслета. Часть диаграммы альфа-паттерна из браслета.
Техника альфа позволяет рисовать на браслете пиксель-арт. А сложные альфа-шаблоны, как правило, намного больше, чем удобно носить на запястье. Он фактически становится своего рода миниатюрным гобеленом макраме.
Так что я хотел попробовать свои силы в этом. Поскольку мне сейчас за тридцать, а дружба уже не та, что раньше, я не совсем знала, какой браслет сделать. К счастью, мой малыш любит фильмы Миядзаки, поэтому я сделала ему этот браслет без лица.
No Face, сделанный по этой выкройке.
Немного грубовато по краям, но неплохо для моего первого. А малышу все равно. Он просто счастлив иметь безликого друга. После этого я начал работу над новой выкройкой, которая на данный момент готова примерно на 80%. Продолжая японскую тему, это интерпретация модели Great Wave компании Hokusai.
Большая волна, из этой выкройки.
Если вы присмотритесь, то увидите несколько мест, где я накосячил, худшее из них — это нижний правый угол, где я перетянул несколько стежков по краю, из-за чего край стал наклонным. Поскольку этот был таким большим, я прикрепил конец к маленькому стержню, что сделало его похожим на свиток.
Опять же, поскольку альфа-браслеты представляют собой гобелены с пиксельной графикой, я подумал, почему бы не повесить их на стену и не сделать крошечную галерею. И всегда есть горстка современных художников, чье искусство я обожаю, но чьи цены слишком высоки, или чьи лучшие произведения были проданы, и которые не печатают. Так что я никогда не смогу повесить на стену. Возьмем, к примеру, Келли Римтсен, известную своими драматическими позами женщин в красочных платьях 50-х годов с электроинструментами. Несколько лет назад я отправил ей электронное письмо с вопросом о принтах, и она ответила: «Я не делаю принты». Сегодня она, по-видимому, так и делает, но до сих пор крайне сложно найти какие-либо репродукции ее хороших произведений.
Так что я никогда не смогу повесить на стену. Возьмем, к примеру, Келли Римтсен, известную своими драматическими позами женщин в красочных платьях 50-х годов с электроинструментами. Несколько лет назад я отправил ей электронное письмо с вопросом о принтах, и она ответила: «Я не делаю принты». Сегодня она, по-видимому, так и делает, но до сих пор крайне сложно найти какие-либо репродукции ее хороших произведений.
Когда я впервые увидел одно из ее произведений (в ресторане на улице Ньюбери в Бостоне), оно меня поразило. Но поскольку я накопил достаточно денег, чтобы позволить себе то, что раньше стоило ее искусство, так и она приобрела достаточно славы, чтобы ее цены постоянно оставались непрактичными. Я даже пытался нарисовать свою собственную имитацию одной из ее картин, хотя это не так уж хорошо.
Вместо этого я решил преобразовать одну из ее работ в пиксель-арт и сам связать гобелен для браслета дружбы. Вот мой пиксель-арт в процессе. Его все еще нужно немного почистить, и я не знаю, как добиться точного цвета ниток, но я работаю над этим.
